题目内容
抛物线y=kx2+2x-5与x轴两个交点的横坐标之和为6，则它们的积为________．
15
分析：由题意令y=0，得方程kx2+2x-5=0，根据根与系数的关系及已知抛物线x轴两个交点的横坐标之和为6，可得x1+x2=6，求出k值，从而求解；
解答：令y=0，得方程=kx2+2x-5=0，
设方程的根为x1，x2，
∵抛物线y=kx2+2x-5与x轴两个交点的横坐标之和为6，
∴x1+x2=-
=6，
∴k=-
，
∴x1x2=
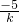=15，
故答案为15．
点评：此题主要考查抛物线的基本性质，解题的关键是求出抛物线的解析式，再利用根与系数求解，把函数的方程结合起来出题，是一种比较好的题型．
分析：由题意令y=0，得方程kx2+2x-5=0，根据根与系数的关系及已知抛物线x轴两个交点的横坐标之和为6，可得x1+x2=6，求出k值，从而求解；
解答：令y=0，得方程=kx2+2x-5=0，
设方程的根为x1，x2，
∵抛物线y=kx2+2x-5与x轴两个交点的横坐标之和为6，
∴x1+x2=-
=6，∴k=-
，∴x1x2=
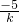=15，故答案为15．
点评：此题主要考查抛物线的基本性质，解题的关键是求出抛物线的解析式，再利用根与系数求解，把函数的方程结合起来出题，是一种比较好的题型．
练习册系列答案
相关题目
已知抛物线y=kx2（k＞0）与直线y=ax+b（a≠0）有两个公共点，它们的横坐标分别为x1、x2，又有直线y=ax+b与x轴的交点坐标为（x3，0），则x1、x2、x3满足的关系式是（ ）
| A、x1+x2=x3 | ||||||
B、
| ||||||
C、x3=
| ||||||
| D、x1x2+x2x3=x1x3 |
已知：抛物线y=kx2+2（k+1）x+k+1开口向下，且与x轴有两个交点，则k的取值范围是（ ）
| A、-1＜k＜0 | B、k＜0 | C、k＜-1 | D、k＞-1 |