题目内容
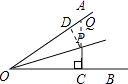
【题目】如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是 . 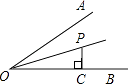
【答案】4﹣2 ![]()
【解析】解:延长CP,与OA交于点Q,过P作PD⊥OA, ∵OP平分∠AOB,PD⊥OA,PC⊥OB,
∴PD=PC,
在Rt△QOC中,∠AOB=30°,OC=2,
∴QC=OCtan30°=2× ![]() =
= ![]() ,∠APD=30°,
,∠APD=30°,
在Rt△QPD中,cos30°= ![]() =
= ![]() ,即PQ=
,即PQ= ![]() DP=
DP= ![]() PC,
PC,
∴QC=PQ+PC,即 ![]() PC+PC=
PC+PC= ![]() ,
,
解得:PC=4﹣2 ![]() .
.
所以答案是:4﹣2 ![]() .
.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
相关题目