题目内容
(1)如图,△ABC三点的坐标分别为A(2,2),B(6,2),C(3,4),△ABC关于x轴作轴对称变换得到△DEF,则点A的对应点的坐标为______;(2)△ABC绕原点逆时针旋转90°得到△MNT,则点B的对应点的坐标为______;
(3)画出△DEF与△MNT,则△DEF与△MNT关于直线______对称.

【答案】分析:(1)由轴对称的性质知,线段AD的垂直平分线为对称轴,画出对称图形结合坐标轴可得出答案.
(2)连接点(0,0)和各点A,逆时针旋转90°,即可得到各点的对应点,顺次连接可得出△MNT,继而也可得到点B的对应点的坐标.
(3)画出图形后可直接观察出答案.
解答:解:由图形可得:(1)点A(2,-2);
(2)点N(-2,6);
(3)通过观察图形可得△DEF与△MNT关于直线yx对称.
故答案为:(2,-2)、(-2,6)、y=x.

点评:本题考查轴对称和旋转对称,并且与一次函数的知识相综合,是一道难度较大的题目,解答本题要注意掌握两种几何变换的特点.
(2)连接点(0,0)和各点A,逆时针旋转90°,即可得到各点的对应点,顺次连接可得出△MNT,继而也可得到点B的对应点的坐标.
(3)画出图形后可直接观察出答案.
解答:解:由图形可得:(1)点A(2,-2);
(2)点N(-2,6);
(3)通过观察图形可得△DEF与△MNT关于直线yx对称.
故答案为:(2,-2)、(-2,6)、y=x.

点评:本题考查轴对称和旋转对称,并且与一次函数的知识相综合,是一道难度较大的题目,解答本题要注意掌握两种几何变换的特点.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
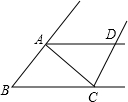 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
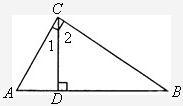
 ,且CB=CE.
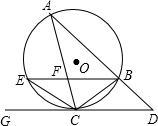
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.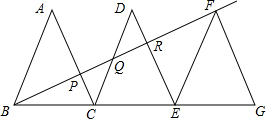 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且