题目内容
已知正三角形A1B1C1的边长为1,作△A1B1C1的内切圆⊙O,再作⊙O的内接正三角形A2B2C2,继续作△A2B2C2的内切圆,…,如此作下去,则正三角形AnBnCn的边长为( )A.

B.

C.

D.不能确定
【答案】分析:根据题意,得内接正三角形A2B2C2的边心距是正三角形A1B1C1的边心距的 ,根据两个三角形相似,得它们的边长比也是
,根据两个三角形相似,得它们的边长比也是 ,则正三角形AnBnCn的边长是
,则正三角形AnBnCn的边长是 .
.
解答:解:∵正三角形A1B1C1的边长为1,
∴内接正三角形A2B2C2的边心距是正三角形A1B1C1的边心距的 ,
,
又∵两个三角形相似,
∴它们的边长比也是 ,
,
∴正三角形AnBnCn的边长是 .
.
故选B
点评:注意:所有的正三角形相似,且相似比等于它们的边心距的比.
 ,根据两个三角形相似,得它们的边长比也是
,根据两个三角形相似,得它们的边长比也是 ,则正三角形AnBnCn的边长是
,则正三角形AnBnCn的边长是 .
.解答:解:∵正三角形A1B1C1的边长为1,
∴内接正三角形A2B2C2的边心距是正三角形A1B1C1的边心距的
 ,
,又∵两个三角形相似,
∴它们的边长比也是
 ,
,∴正三角形AnBnCn的边长是
 .
.故选B
点评:注意:所有的正三角形相似,且相似比等于它们的边心距的比.

练习册系列答案
相关题目
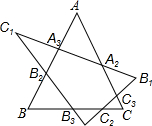
 7、如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1.
7、如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1. 如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1.
如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1.