Question

【题目】以C为直角顶点的两个等腰直角△CAB和△CDG，E为AB的中点，F为DG的中点．

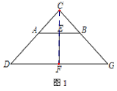
（1）如图1，点A、B分别在边CD，CG上，则EF与AD的数量关系是______________；

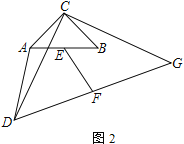
（2）如图2，点A、B不在边CD、CG上，（1）中EF与AD的关系还成立吗?请证明你的结论；

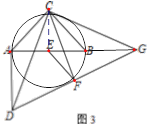
（3）如图3，若A、B、G在同一直线上，且A、C、B、F在同一圆上，直接写出△CDG与△CAB面积之比．

Answer 1

【答案】（1）AD=EF；（2）成立，证明见解析；（3）．

【解析】试题分析：（1）连接CE、CF，证明C、E、F三点共线，然后在Rt△ACE中，由∠A=45°，可得AC=CE，同理，DC=CF，再根据AD=CD-AC，推导即可得；

（2）成立，连接CE、CF，通过证明△ACD∽△ECF，根据相似三角形对应边成比例即可得；

（3）连接CE，由A、C、B、F在同一圆上，可知点E为圆心，从而可得CE=EF，再由（2）AD=EF、AC=CE从而可得AC=AD，由已知可得△ACD≌△BCG，从而可得∠ADC=∠AGB=22.5°，可得∠DAG=90°，设AE=x，则AB =2x，AG=2x+x，AD=x，由勾股定理DG2= (8+4)x2，再由△CDG∽△CAB，可得.

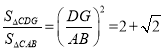试题解析：（1）如图（1）连接CE，CF，

∵CA=CB，CD=CG，E为AB中点，F为DG中点，∴CE⊥AB，CF⊥DG，

∵∠C=90°，∴∠CAB=∠CDG=45°，∴AB//DG，∴C、E、F三点共线，

在Rt△ACE中，∠A=45°，∴AC=CE，

同理，DC=CF，

∵AD=CD-AC，EF=CF-CE，

∴AD=EF，

故答案为：AD=EF；

（2）成立．

连接CE、CF，

∵∠ACB=∠DCG=90°，CA=CB，CD=CG，AE=BE，DF=GF，

∴∠ACE=45°，∠DCF=45°，∠CAB=∠CDG=45°，∠AEC=∠DFC=90°，

∴∠ACD=∠ECF，

在Rt△ACE中，∠CAE=45°，∴AC=CE，

同理，DC=CF，

∴AC：CE=DC：CF，

∴△ACD∽△ECF，∴AD：EF=AC：CE=，

∴AD=EF；

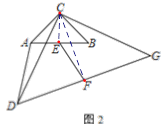
（3）连接CE，

∵A、C、B、F四点共圆，∠ACB=90°，AE=EB，∴E为圆心，

∴AE=CE=EF=BE，

∵∠ACB=∠DCG=90°，∴∠ACD=∠BCG，

∵AC=BC，DC=GC，∴△ACD≌△BCG，

∴BG=AD，∠CDA=∠CGB，

由（2）AD=EF、AC=CE，∴AD=AC，

∴CB=BG，∴∠BCG=∠BGC，

∵∠BCG+∠BGC=∠ABC=45°，

∴∠BGC=22.5°，

∴∠ADC=22.5°，

∵∠CGD=∠CDG=45°，∴∠AGD=22.5°，

∴∠AGD+∠CDG+∠ADC=90°，

∴∠DAG=90°，

设AE=x，则AB =2x，AG=2x+x，AD=x，

由勾股定理DG2=AD2+AG2，

∴DG2=（x）2+（2x+x）2=(8+4)x2，

∵△CDG∽△CAB，

∴.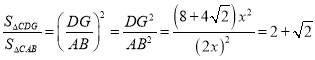