题目内容
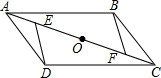 如图,将△ADC绕AC的中点O旋转180°,得到△CBA,分别在AC上取点E、F,使得AE=CF,连接DE、BF.
如图,将△ADC绕AC的中点O旋转180°,得到△CBA,分别在AC上取点E、F,使得AE=CF,连接DE、BF.
(1)求证:△ADE≌△CBF;
(2)连接BE、DF,求证:四边形DEBF是平行四边形;
(3)当△ADC满足______条件时,平行四边形DEBF是菱形?(直接填条件,不用证明)
(1)证明:∵△ADC绕AC的中点O旋转180°,得到△CBA,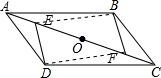
∴AD=CB,∠DAC=∠BCA,
在△ADE和△CBF中,
∵ ,
,
∴△ADE≌△CBF(SAS);
(2)证明:连BE、CF,
∵△ADE≌△CBF,
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°-∠AED,∠BFE=180°-∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
(3)当DA=DC时,平行四边形DEBF是菱形.理由如下:
∵DA=DC,
∴∠DAE=∠DCF,
在△DAE和△DCF中,
∵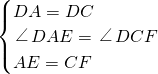 ,
,
∴△DAE≌△DCF,
∴DE=DF,
∴平行四边形DEBF是菱形.
故答案为:DA=DC.
分析:(1)根据旋转的性质得到AD=CB,∠DAC=∠BCA,而AE=CF,根据全等三角形的判定方法易得△ADE≌△CBF;
(2)连BE、CF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论;
(3)当DA=DC时,则∠DAE=∠DCF,易整得△DAE≌△DCF,得到DE=DF,根据菱形的判定即可得到平行四边形DEBF是菱形.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了全等三角形的判定与性质、平行四边形的判定以及菱形的判定.

∴AD=CB,∠DAC=∠BCA,
在△ADE和△CBF中,
∵
 ,
,∴△ADE≌△CBF(SAS);
(2)证明:连BE、CF,
∵△ADE≌△CBF,
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°-∠AED,∠BFE=180°-∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
(3)当DA=DC时,平行四边形DEBF是菱形.理由如下:
∵DA=DC,
∴∠DAE=∠DCF,
在△DAE和△DCF中,
∵
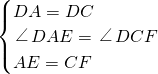 ,
,∴△DAE≌△DCF,
∴DE=DF,
∴平行四边形DEBF是菱形.
故答案为:DA=DC.
分析:(1)根据旋转的性质得到AD=CB,∠DAC=∠BCA,而AE=CF,根据全等三角形的判定方法易得△ADE≌△CBF;
(2)连BE、CF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论;
(3)当DA=DC时,则∠DAE=∠DCF,易整得△DAE≌△DCF,得到DE=DF,根据菱形的判定即可得到平行四边形DEBF是菱形.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了全等三角形的判定与性质、平行四边形的判定以及菱形的判定.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目



 的度数;②当
的度数;②当
 (0°<
(0°<

 (0°<
(0°<