题目内容
 如图,等边三角形的边长为6,则高AD的长为( )
如图,等边三角形的边长为6,则高AD的长为( )分析:由等边三角形的性质可知三边长都为6,再利用等腰三角形的三线合一性质,由AD与BC垂直得到D为BC的中点,进而由BCd的长求出BD的长,在直角三角形ABD中,由AB及BD的长,利用勾股定理即可求出AD的长.
解答:解:∵△ABC为边长为6的等边三角形,且AD⊥BC,(已知)
∴AB=AC=BC=6,(等边三角形的三边长相等)
∴BD=CD=
BC=3,(三线合一)
在Rt△ABD中,由AB=6,BD=3,
根据勾股定理得:AD=
=3
.
故选C
∴AB=AC=BC=6,(等边三角形的三边长相等)
∴BD=CD=
| 1 |
| 2 |
在Rt△ABD中,由AB=6,BD=3,
根据勾股定理得:AD=
| AB2-BD2 |
| 3 |
故选C
点评:此题考查了等腰三角形及等边三角形的性质,以及勾股定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
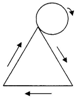 (2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
(2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
 的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A
的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A B
B 为y,则y关于x的函数图象大致为(
)
为y,则y关于x的函数图象大致为(
)

