题目内容
 如图,点A(1,0),B(0,
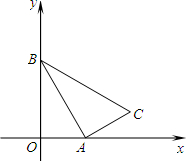
如图,点A(1,0),B(0, )分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
)分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求直线AB的解析式及点C的坐标;
(2)若点P(m, )为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
)为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
 解:(1)设直线AB的解析式为y=kx+b则
解:(1)设直线AB的解析式为y=kx+b则 ,
,解得k=-
 ,b=
,b=
∴y=-
 x+
x+ ,
,作CD⊥x轴,垂足为D,
∵OA=1,OB=
 ,
,∴AB=2
∵∠ABC=30°,
∴AC=
 ,
,∵
 ,
,∴∠OAB=60°,
∴∠CAD=30°
∴CD=
 ,AD=1,
,AD=1,∴C的坐标是
 ,
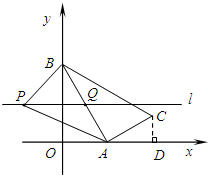
,(2)如图,过点P作直线l∥x轴,交AB于点Q,则点Q的坐标是
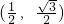
S△ABC=
 AB•AC=
AB•AC= ×2×
×2× =
= ,
,S△ABC=S△APB,
∴
 ×PQ•OB=
×PQ•OB= ,即
,即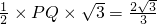 ,
,解得PQ=
 ,
,∴
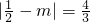 ,
,解得m1=
 ,m2=-
,m2=- .
.分析:(1)设直线AB的解析式为y=kx+b,根据条件列出二元一次方程组,求出k和b的值,作CD⊥x轴,垂足为D,即可求出C点坐标;
(2)如图,过点P作直线l∥x轴,交AB于点Q,求出点Q的坐标,先求出三角形ABC的面积的值,然后令两面积相等,求出PQ的值,进而求出m的值.
点评:本题主要考查一次函数的综合题,解答本题的关键是熟练掌握一次函数的性质,并结合图形进行答题,此题是中考的重点题型,此题难度不大.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是