题目内容
 如图所示,在直角坐标系中,矩形ABCD的顶点A (1,0),对角线的交点P(
如图所示,在直角坐标系中,矩形ABCD的顶点A (1,0),对角线的交点P(| 5 | 2 |
(1)写出B、C、D三点的坐标;
(2)若在线段AB上有一点 E(3,0),过E点的直线将矩形ABCD的面积分为相等的两部分,求直线的解析式;
(3)若过C点的直线l将矩形ABCD的面积分为4:3两部分,并与y轴交于点M,求M点的坐标.
分析:(1)由矩形的性质结合顶点A (1,0),对角线的交点P(
,1),利用中点坐标公式即可求出C点坐标,同理求出C和D点坐标;
(2)设直线解析式为y=kx+b,若过E点的直线将矩形ABCD的面积分为相等的两部分,则直线必定过P点,求出k和b的值即可;
(3)首先求出矩形的面积,过C点的直线l将矩形ABCD的面积分为4:3两部分,求出直线与AD或AB的交点坐标,分别设出直线的解析式,求出对应的系数,即可求出M点的坐标.
| 5 |
| 2 |
(2)设直线解析式为y=kx+b,若过E点的直线将矩形ABCD的面积分为相等的两部分,则直线必定过P点,求出k和b的值即可;
(3)首先求出矩形的面积,过C点的直线l将矩形ABCD的面积分为4:3两部分,求出直线与AD或AB的交点坐标,分别设出直线的解析式,求出对应的系数,即可求出M点的坐标.
解答:解:(1)∵四边形ABCD是矩形,顶点A (1,0),对角线的交点P(
,1),
∴
=
,yD=2,
∴C点坐标为(4,2),B点坐标为(4,0),D点坐标为(1,2);
(2)设直线解析式为y=kx+b,
∵过E点的直线将矩形ABCD的面积分为相等的两部分,
∴该直线经过点P(
,1),
由题意得
,
解得k=-2,b=6,
∴直线解析式为y=-2x+6;
(3)由题意知,矩形ABCD的面积为6,如图1
∵过C点的直线l将矩形ABCD的面积分为4:3两部分,
∴S△CDN=
DC•DN=
×3×DN=
×6,
∴DN=
,
∴N点坐标为(1,
),
∴直线经过N点和C点,
设经过AD边的直线解析式为y=mx+n,
由题意得
,
解得m=
,n=-
,
∴直线与y轴交点M的坐标为(0,-
);
过C点的直线l将矩形ABCD的面积分为4:3两部分,如图2
∴S△CBN=
BC•BN=
×2×BN=
×6,
解得BN=
,
∴AN=
,
∴N点坐标为(
,0),
设经过AB边的直线解析式为y=ax+b,
由题意得
,
解得a=
,b=-
,
∴直线与y轴交点M的坐标为(0,-
);
综上所述M点坐标为(0,-
)或(0,-
).
| 5 |
| 2 |
∴
| 1+xC |
| 2 |
| 5 |
| 2 |
∴C点坐标为(4,2),B点坐标为(4,0),D点坐标为(1,2);
(2)设直线解析式为y=kx+b,
∵过E点的直线将矩形ABCD的面积分为相等的两部分,
∴该直线经过点P(
| 5 |
| 2 |
由题意得
|
解得k=-2,b=6,
∴直线解析式为y=-2x+6;
(3)由题意知,矩形ABCD的面积为6,如图1
∵过C点的直线l将矩形ABCD的面积分为4:3两部分,

∴S△CDN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 7 |
∴DN=
| 12 |
| 7 |
∴N点坐标为(1,
| 2 |
| 7 |
∴直线经过N点和C点,
设经过AD边的直线解析式为y=mx+n,
由题意得
|
解得m=
| 4 |
| 7 |
| 2 |
| 7 |
∴直线与y轴交点M的坐标为(0,-
| 2 |
| 7 |
过C点的直线l将矩形ABCD的面积分为4:3两部分,如图2

∴S△CBN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 7 |
解得BN=
| 18 |
| 7 |
∴AN=
| 3 |
| 7 |
∴N点坐标为(
| 10 |
| 7 |
设经过AB边的直线解析式为y=ax+b,
由题意得
|
解得a=
| 7 |
| 9 |
| 10 |
| 9 |
∴直线与y轴交点M的坐标为(0,-
| 10 |
| 9 |
综上所述M点坐标为(0,-
| 2 |
| 7 |
| 10 |
| 9 |
点评:本题主要考查一次函数的综合题的知识,解答本题的关键是熟练掌握中点坐标公式以及函数解析式的求法,特别是第(3)小问有两种可能性,此题难度不大,但是常考的试题.

练习册系列答案
相关题目
 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.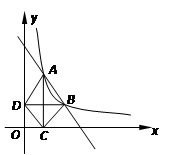

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.