题目内容
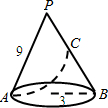 已知,如图,圆锥的底面圆的半径为3cm,母线长为9cm,C为母线PB的中点,一只蚂蚁欲从点A处沿圆锥的侧面爬到C处,则它爬行最短距离为
已知,如图,圆锥的底面圆的半径为3cm,母线长为9cm,C为母线PB的中点,一只蚂蚁欲从点A处沿圆锥的侧面爬到C处,则它爬行最短距离为分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
解答: 解:圆锥的底面周长是6π,则6π=
解:圆锥的底面周长是6π,则6π=
∴n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°
则在圆锥侧面展开图中AP=9,PC=4.5,∠ACP=90度.
∴在圆锥侧面展开图中AC=
=
cm.
故答案为
cm.
 解:圆锥的底面周长是6π,则6π=
解:圆锥的底面周长是6π,则6π=| nπ×9 |
| 180 |
∴n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°
则在圆锥侧面展开图中AP=9,PC=4.5,∠ACP=90度.
∴在圆锥侧面展开图中AC=
| AP2-PC2 |
| 9 |
| 2 |
| 3 |
故答案为
| 9 |
| 2 |
| 3 |
点评:本题需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.

练习册系列答案
相关题目
 已知:如图,圆锥的母线长OA=6,底面圆的半径为
已知:如图,圆锥的母线长OA=6,底面圆的半径为 已知,如图,圆锥的底面圆的半径为3cm,母线长为9cm,C为母线PB的中点,一只蚂蚁欲从点A处沿圆锥的侧面爬到C处,则它爬行最短距离为________.
已知,如图,圆锥的底面圆的半径为3cm,母线长为9cm,C为母线PB的中点,一只蚂蚁欲从点A处沿圆锥的侧面爬到C处,则它爬行最短距离为________.
