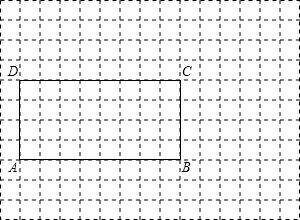
题目内容
在如图所示正方形网格中,每个小正方形的边长为1.(1)画出矩形ABCD绕B点顺时针旋转90°的图形A′B′C′D′;
(2)求线段DA′和AD′的长度.

【答案】分析:(1)由矩形ABCD绕B点顺时针旋转90°可得BA⊥BA′,BC⊥BC′,AD⊥A′D′,CD⊥C′D′,BA=BA′,BC=BC′,AD=A′D′,CD=C′D′,由此可以画出矩形A′BC′D′;
(2)连接DA′、AD′,由图形可知,DA′= ,AD′=
,AD′= ,可求出DA′与AD′的值.
,可求出DA′与AD′的值.
解答:解:(1)∵矩形ABCD绕B点顺时针旋转90°
∴BA⊥BA′,BC⊥BC′,AD⊥A′D′,CD⊥C′D′,
BA=BA′,BC=BC′,AD=A′D′,CD=C′D′,
∴可以画出矩形A′BC′D′,如下图所示:

(2)连接DA′、AD′,如下图所示:

由图形可知,DA′= =
= =4
=4 ,
,
AD′= =
= =4
=4 .
.
点评:本题主要考查了旋转变换后的作图,要结合勾股定理进行相应计算.
(2)连接DA′、AD′,由图形可知,DA′=
 ,AD′=
,AD′= ,可求出DA′与AD′的值.
,可求出DA′与AD′的值.解答:解:(1)∵矩形ABCD绕B点顺时针旋转90°
∴BA⊥BA′,BC⊥BC′,AD⊥A′D′,CD⊥C′D′,
BA=BA′,BC=BC′,AD=A′D′,CD=C′D′,
∴可以画出矩形A′BC′D′,如下图所示:

(2)连接DA′、AD′,如下图所示:

由图形可知,DA′=
 =
= =4
=4 ,
,AD′=
 =
= =4
=4 .
.点评:本题主要考查了旋转变换后的作图,要结合勾股定理进行相应计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目