题目内容
我们知道:对于任何实数 ,①∵
,①∵ ≥0,∴
≥0,∴ +1>0;②∵
+1>0;②∵ ≥0,∴
≥0,∴ +
+ >0.
>0.
模仿上述方法解答:
求证:(1)对于任何实数 ,均有:
,均有: >0;
>0;
(2)不论 为何实数,多项式
为何实数,多项式 的值总大于
的值总大于 的值.
的值.
【答案】
见解析
【解析】
试题分析:(1)将代数式前两项提取2,配方后根据完全平方式为非负数,得到代数式大于等于1,即对于任何实数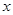 ,代数式
,代数式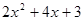 的值总大于0,得证.
的值总大于0,得证.
(2)将代数式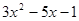 减去
减去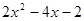 ,然后配方根据完全平方式为非负数,得到代数式大于等于
,然后配方根据完全平方式为非负数,得到代数式大于等于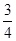 ,即对于任何实数
,即对于任何实数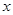 ,多项式
,多项式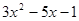 的值总大于
的值总大于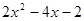 .
.
解:(1)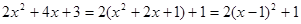
∵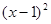 ≥0 ∴
≥0 ∴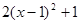 >0 ∴
>0 ∴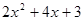 >0……3分
>0……3分
(2)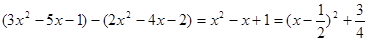
∵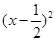 ≥0 ∴
≥0 ∴ >0
>0
∴ >0
>0
即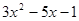 >
>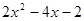
考点:配方法的应用;非负数的性:偶次方.
点评:此题考查了配方法的应用,以及非负数的性质:偶次幂,灵活应用完全平方公式是解本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 ,①∵
,①∵ ≥0,∴
≥0,∴ ≥0,∴
≥0,∴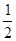 >0.
>0. >0;
>0; 的值总大于
的值总大于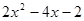 的值.
的值. =(x-1)2+
=(x-1)2+ >0;模仿上述方法解答:
>0;模仿上述方法解答: