题目内容
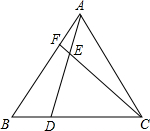 如图,△ABC是等边三角形,D,F分别是BC,AB上的点,且BD=AF,AD,CF交于点E,则∠CED=________度.
如图,△ABC是等边三角形,D,F分别是BC,AB上的点,且BD=AF,AD,CF交于点E,则∠CED=________度.
60
分析:根据全等三角形的判定定理SAS推知△ABD≌△CAF;然后由全等三角形的对应角相等知∠ACF=∠BAD;最后根据等边三角形的性质、三角形的外角定理求得∠CED=∠ACF+∠EAC,即
∠CAF=60°.
解答: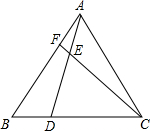 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴∠ABD=∠CAF=60°,AB=CA,
在△ABD和△CAF中,
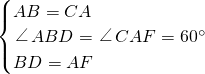 ,
,
∴△ABD≌△CAF(SAS),
∴∠ACF=∠BAD(全等三角形的对应角相等);
又∵∠CED=∠ACF+∠EAC(外角定理),
∴∠CED=∠CAF=60°.
故答案是:60.
点评:本题考查了等边三角形的性质、全等三角形的判定与性质.可围绕结论寻找全等三角形,运用全等三角形的性质判定所对应的角相等.
分析:根据全等三角形的判定定理SAS推知△ABD≌△CAF;然后由全等三角形的对应角相等知∠ACF=∠BAD;最后根据等边三角形的性质、三角形的外角定理求得∠CED=∠ACF+∠EAC,即
∠CAF=60°.
解答:
 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,∴∠ABD=∠CAF=60°,AB=CA,
在△ABD和△CAF中,
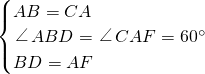 ,
,∴△ABD≌△CAF(SAS),
∴∠ACF=∠BAD(全等三角形的对应角相等);
又∵∠CED=∠ACF+∠EAC(外角定理),
∴∠CED=∠CAF=60°.
故答案是:60.
点评:本题考查了等边三角形的性质、全等三角形的判定与性质.可围绕结论寻找全等三角形,运用全等三角形的性质判定所对应的角相等.

练习册系列答案
相关题目
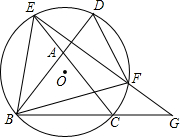 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.