Question

【题目】已知的边与x轴重合，，反比例函数在第一象限内的图象与边交于点，与AB边交于点，的面积为2.

（1）直接写出之间的数量关系 ；当时，求反比例函数及直线的表达式；

（2）设直线与y轴交于点F,点P在射线FD上，在（1）的条件下，如果与相似，求点的坐标.

Answer 1

【答案】(1) n=2m；反比例函数的解析式为y=，直线AB的函数解析式为y=x+1.

(2) (1,1)或(5,1).

【解析】

（1）将D（4，m）、E（2，n）代入反比例函数解析式，进而得出n，m的关系；利用△BDE的面积为2，得出m的值，进而得出D，E，B的坐标，利用待定系数法求出一次函数与反比例函数关系式即可；

（2）利用△AEO与△EFP 相似存在两种情况，分别利用图形分析得出即可．

(1)∵D(4,m)、E(2,n)在反比例函数的图象上，

∴.

整理，得n=2m；

如图1，过点E作EH⊥BC，垂足为H.

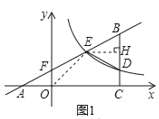
在Rt△BEH中,tan∠BEH=tan∠A=，

因为EH=2，所以BH=1.

因此D(4,m),E(2,2m),B(4,2m+1).

已知△BDE的面积为2，

所以BD·EH= (m+1)×2=2.

解得m=1.

因此D(4,1),E(2,2),B(4,3).

因为点D(4,1)在反比例函数的图象上，

所以k=4.

因此反比例函数的解析式为y=，

设直线AB的解析式为y=kx+b,代入B(4,3)、E(2,2)，

得，

解得，

因此直线AB的函数解析式为y=x+1.

(2)∵AB解析式为y=x+1.

∴A（-2,0），F（0，1），又D(4,1),E(2,2),B(4,3).

∴AE=2，EF=

因为直线y=x+1与y轴交于点F(0,1),点D的坐标为(4,1)，

所以FD∥x轴,∠EFP=∠EAO.

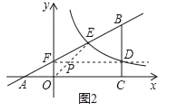
因此△AEO与△EFP 相似存在两种情况：

①如图2,当时,

解得FP=1.此时点P的坐标为(1,1).

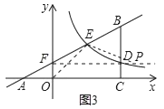
②如图3,当时,.

解得FP=5.

此时点P的坐标为(5,1).

综上所述,P点坐标为：(1,1)或(5,1).