题目内容
 如图,把斜边长为
如图,把斜边长为| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
分析:根据勾股定理可得,AB=BD=2,则AE=BE=BC=CD=1,所以,S△AEF=S△BEF=S△BCF=S△CDF,即S△CDF=
S△ABC,则两纸片覆盖桌面的面积=S△ABC+S△CDF,解答出即可.
| 1 |
| 3 |
解答: 解:∵AC=
解:∵AC=
,BC=1,
∴AB=2,
即AB=BD=2,BC=AE=BE=CD=1,
∵△ABC≌△DBE,
∴S△AEF=S△BEF=S△BCF=S△CDF,
即S△CDF=S△AEF,
又∵S△ABC=
×1×2=1,
∴S△CDF=
,
∴两纸片覆盖桌面的面积=S△ABC+S△CDF=1+
=
.
故答案为:
.
 解:∵AC=
解:∵AC=| 5 |
∴AB=2,
即AB=BD=2,BC=AE=BE=CD=1,
∵△ABC≌△DBE,
∴S△AEF=S△BEF=S△BCF=S△CDF,
即S△CDF=S△AEF,
又∵S△ABC=
| 1 |
| 2 |
∴S△CDF=
| 1 |
| 3 |
∴两纸片覆盖桌面的面积=S△ABC+S△CDF=1+
| 1 |
| 3 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查了直角三角形的性质和三角形的等积变换,掌握等底等高的两个三角形的面积相等.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 动点.
动点. (2013•昆山市二模)如图,把一个斜边长为2且含有30°角的直角三角形ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积为
(2013•昆山市二模)如图,把一个斜边长为2且含有30°角的直角三角形ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积为
 如图,把斜边长为
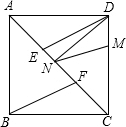
如图,把斜边长为 ,一直角边长为1的两全等直角三角形纸片如图摆在桌面上,使直角重合,则两纸片覆盖桌面的面积是________.
,一直角边长为1的两全等直角三角形纸片如图摆在桌面上,使直角重合,则两纸片覆盖桌面的面积是________.