Question

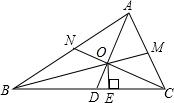
如图，△ABC的三条内角平分线相交于点O，过点O作OE⊥BC于E点，求证：∠BOD=∠COE．

Answer 1

证明：∵∠AFO=∠FBC+∠ACB=

1

2

∠ABC+∠ACB，
∴∠AOF=180°-（∠DAC+∠AF0）
=180°-[

1

2

∠BAC+

1

2

∠ABC+∠ACB]
=180°-[

1

2

（∠BAC+∠ABC）+∠ACB]
=180°-[

1

2

（180°-∠ACB）+∠ACB]
=180°-[90°+

1

2

∠ACB]
=90°-

1

2

∠ACB，
∴∠BOD=∠AOF=90°-

1

2

∠ACB，
又∵在直角△OCE中，∠COE=90°-∠OCD=90°-

1

2

∠ACB，
∴∠BOD=∠COE．