题目内容
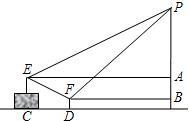 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留到0.1米)
分析:由于气球的高度为PA+AB+FD,而AB=1米,FD=0.5米,可设PA=h米,根据题意,列出关于h的方程可求解.
解答:解:设AP=h米,(1分)
∵∠PFB=45°,
∴BF=PB=h+1,(2分)
∴EA=BF+CD=h+1+5=h+6,(3分)
在Rt△PEA中,PA=AE•tan30°,
∴h=(h+6)tan30°,(5分)
3h=(h+6)
,
h=
=
=
≈8.2,(6分)
∴气球的高度为PA+AB+FD=8.2+1+0.5=9.7米.(8分)
∵∠PFB=45°,
∴BF=PB=h+1,(2分)
∴EA=BF+CD=h+1+5=h+6,(3分)
在Rt△PEA中,PA=AE•tan30°,
∴h=(h+6)tan30°,(5分)
3h=(h+6)
| 3 |
h=
6
| ||
3-
|
| 6 | ||
|
6(
| ||
| 2 |
∴气球的高度为PA+AB+FD=8.2+1+0.5=9.7米.(8分)
点评:对于此类问题常常转化成直角三角形,可利用三角函数的知识来解决.

练习册系列答案
相关题目
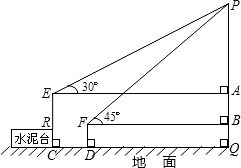 如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据:
如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据: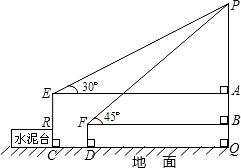 如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据:
如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据: )
)