题目内容
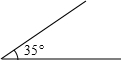 已知“一个三角形的两条边长分别是3cm和4cm,一个内角为35°”,那么满足这一条件,且彼此不全等的三角形共有
已知“一个三角形的两条边长分别是3cm和4cm,一个内角为35°”,那么满足这一条件,且彼此不全等的三角形共有
- A.2个
- B.3个
- C.4个
- D.5个
C
分析:分①3、4是夹35°角的边,②3是35°角的对边,③4是35°角的对边三种情况讨论求解即可.
解答:①3、4是夹35°角的边时,可作1个三角形,
②3是35°角的对边时,可作2个三角形,
③4是35°角的对边时,可作1个三角形,
根据全等三角形的判定方法,以上三角形都是不全等的三角形,
所以,不全等的三角形共有4个.
故选C.
点评:本题考查了全等三角形的判定,难点在于要分情况讨论,并熟记全等三角形的判定方法.
分析:分①3、4是夹35°角的边,②3是35°角的对边,③4是35°角的对边三种情况讨论求解即可.
解答:①3、4是夹35°角的边时,可作1个三角形,
②3是35°角的对边时,可作2个三角形,
③4是35°角的对边时,可作1个三角形,
根据全等三角形的判定方法,以上三角形都是不全等的三角形,
所以,不全等的三角形共有4个.
故选C.
点评:本题考查了全等三角形的判定,难点在于要分情况讨论,并熟记全等三角形的判定方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




