题目内容
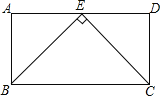
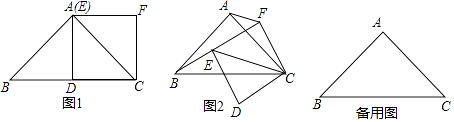
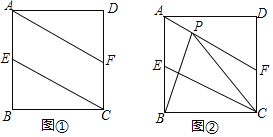
【题目】如图
，矩形ABCD中，
，
，E、F分别是AB、CD的中点
求证：四边形AECF是平行四边形；
是否存在a的值使得四边形AECF为菱形，若存在求出a的值，若不存在说明理由；
如图
，点P是线段AF上一动点且
求证：
；
直接写出a的取值范围．
【答案】（1）证明见解析；（2）不存在；（3）①证明见解析；②
．
【解析】
(1)由矩形性质得
，
，再证
且
即可；（2）不存在，由
知：当
时，四边形AECF为菱形，可得
，此方程无解；（3）由平行线性质得
，证得
，
，由
，
，得OE是三角形的中位线，所以
，根据中垂线性质得
；如图
当P与F重合时，
，
的取值范围是．
证明：
四边形ABCD是矩形，
，，
又
、F分别是边AB、CD的中点，
，
四边形AECF是平行四边形；
解：不存在，
由知：四边形AECF是平行四边形；
当时，四边形AECF为菱形，
四边形ABCD是矩形，
，
，
，
方程无解，故不存在这样的a；
解：
如图
，
四边形AECF是平行四边形，
，
，
，
，
，，
，
，
；
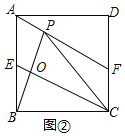
如图，当P与F重合时，，
的取值范围是．
练习册系列答案
阅读快车系列答案
相关题目
