题目内容
18.一个圆锥体形状的水晶饰品,母线长是10cm,底面圆的直径是5cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠绕一圈彩带回到A点,则彩带最少用10$\sqrt{2}$厘米.(接口处重合部分忽略不计)分析 利用圆锥侧面展开图的弧长等于底面圆的周长,进而得出扇形圆心角的度数,再利用勾股定理求出AA′的长.
解答 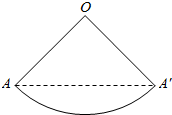 解:由两点间直线距离最短可知,圆锥侧面展开图AA′最短,
解:由两点间直线距离最短可知,圆锥侧面展开图AA′最短,
由题意可得出:OA=OA′=10cm,
$\widehat{A{A}^{'}}=\frac{nπ×10}{180}$=5π,
解得:n=90°,
∴∠AOA′=90°,
∴AA′=$\sqrt{O{A}^{2}+O{{A}^{'}}^{2}}$=10$\sqrt{2}$(cm),
故答案为:10$\sqrt{2}$.
点评 此题主要考查了平面展开图的最短路径问题,得出∠AOA′的度数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若(2m-4)x|2m-3|=8是关于x的一元一次方程,则m的值是( )
| A. | 任何数 | B. | 1 | C. | 2 | D. | 1或2 |
9.计算:2×4×8其结果可记为( )
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
3.支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北,据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学记数法表示为( )
| A. | 4.73×1010 | B. | 47.3×1010 | C. | 4.73×109 | D. | 47.3×109 |
7.宁波轨道交通3号线于2014年12月23日开工建设,预计2020年全线开通,3号线全长32.83千米,32.83千米用科学记数法表示为( )
| A. | 3.283×104米 | B. | 32.83×104米 | C. | 3.283×105米 | D. | 3.283×103米 |
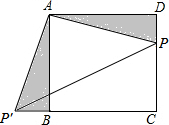 如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=2$\sqrt{5}$.
如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=2$\sqrt{5}$.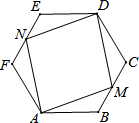 如图,正六边形ABCDEF的边长为1,M、N分别为边BC、EF的中点,则四边形AMDN的面积为$\sqrt{3}$.
如图,正六边形ABCDEF的边长为1,M、N分别为边BC、EF的中点,则四边形AMDN的面积为$\sqrt{3}$. 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.