题目内容
【题目】如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 . 
【答案】( ![]() ,1);y=
,1);y= ![]() x﹣2
x﹣2
【解析】解:如图,过点C′作C′F⊥x轴于点F,
∵△AOC′是等边三角形,OA=2,
∴C′F=1.
在Rt△OC′F中,
由勾股定理,得OF= ![]() =
= ![]() =
= ![]() .
.
∴点C′的坐标为( ![]() ,1).
,1).
∵△AOC′与△ABC都是等边三角形,
∴AO=AC′,AB=AC,∠BAC=∠OAC′=60°,
∴∠BAC﹣∠OAC=∠OAC′﹣∠OAC,
∴∠BAO=∠CAC′,
在△AOB与△AC′C中,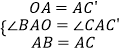
∴△AOB≌△AC′C(SAS).
∴∠BOA=∠CC′A=90°,
∴点C在过点C′且与AC垂直的直线上,
∵点A的坐标是(0,2),△ABC是等边三角形,
∴点C移动到y轴上的坐标是(0,﹣2),
设点C所在的直线方程为:y=kx+b(k≠0).把点( ![]() ,1)和(0,﹣2)分别代入,得
,1)和(0,﹣2)分别代入,得 ![]() ,
,
解得 ![]() ,
,
所以点C移动所得图象的解析式是为:y= ![]() x﹣2.
x﹣2.
所以答案是( ![]() ,1),y=
,1),y= ![]() x﹣2.
x﹣2.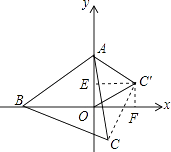

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目