Question

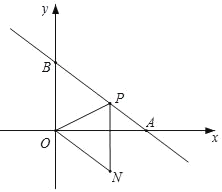
【题目】在平面直角坐标系中，直线y＝﹣x+6分别与x轴、y轴交于点A，B．当点P在线段AB（点P不与A，B重合）上运动时，在坐标系内存在一点N，使得以O，B，P，N为顶点的四边形为菱形．请直接写出N点坐标_____．

Answer 1

【答案】（﹣4，3），（，），（，﹣）．

【解析】

直接考虑以O，B，P，N为顶点的菱形中的数量关系比较复杂,不妨根据菱形的性质,它的一半为等腰三角形,则讨论三边有任意两边相等,分三种情况: BP＝OP, OP＝OB, BP＝OB,再根据坐标系中任意两点间的距离公式列出等式解答即可.

解：∵直线y＝﹣ x+6分别与x轴、y轴交于点A，B，

∴A（8，0），B（0，6）．

分三种情况：

①如图所示，以OB为菱形OPBN的对角线，点P与点N关于OB对称，

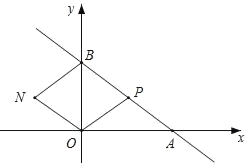
由BP＝OP可得，∠PBO＝∠POB，

根据∠PBO+∠PAO＝∠POB+∠POA＝90°，可得∠POA＝∠PAO，

∴PO＝PA，

∴P是AB的中点，即P（4，3），

∴N（﹣4，3）；

②如图所示，以PB为菱形OPBN的对角线，设P（n，﹣ n+6），

∵四边形OPNB为菱形，B（0，6），

∴OP＝OB＝6＝，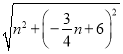

解得：n＝或n＝0（舍去），

∴点P（，），

∴点N（，），即N（，）；

③如图所示，以OP为菱形BPNO的对角线，设P（m，﹣m+6）

∵四边形ONPB为菱形, B（0，6），

∴BP＝OB＝6＝，

解得m＝，

∴P（，），

∴N（，），即N（，﹣），

综上所述，N点坐标为（﹣4，3），（，），（，﹣）．

故答案为：（﹣4，3），（，），（，﹣）．