Question

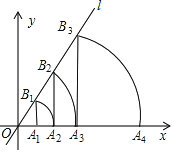
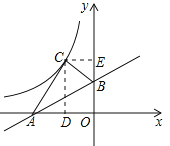
【题目】如图：在平面直角坐标系中，直线AB与轴交于点A（－2，0），与轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线上，则的值（ ）

A. －4 B. －2 C. D.

Answer 1

【答案】D

【解析】设点C的坐标为（x，y），过点C作CD⊥x轴，作CE⊥y轴，由折叠的性质易得∠CAB=∠OAB=30°，AC=AO=2，∠ACB=AOB=90°，用锐角三角函数的定义得CD，CE，得点C的坐标，易得k．

设点C的坐标为（x，y），过点C作CD⊥x轴，作CE⊥y轴．

∵将△ABO沿直线AB翻折，∴∠CAB=∠OAB=30°，AC=AO=2，∠ACB=∠AOB=90°，∴CD=y=ACsin60°=2×=．

∵∠ACB=∠DCE=90°，∴∠BCE=∠ACD=30°．

∵BC=BO=AOtan30°=2×=，CE=|x|=BCcos30°==1．

∵点C在第二象限，∴x=﹣1．

∵点C恰好落在双曲线y=（k≠0）上，∴k=xy=﹣1×=﹣．

故选D．