题目内容
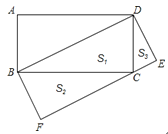
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,
则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出图中的三对相似三角形,并选择其中一对进行证明.
【答案】(1)、![]() ;(2)、△BCD∽△CFB∽△DEC;证明过程见解析.
;(2)、△BCD∽△CFB∽△DEC;证明过程见解析.
【解析】
试题分析:(1)、根据题意得出三个面积之间的关系;(2)、△BCD∽△CFB∽△DEC,根据同角的余角相等得出∠EDC=∠CBD,然后根据垂直得出三角形相似.
试题解析:(1)、![]() .
.
(2)、△BCD∽△CFB∽△DEC.
可任选一对,如:△BCD∽△DEC;
∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,∴△BCD∽△DEC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目