题目内容
20. 如图,AB=CD,AD=BC,E,F是AC上两点,且AE=CF,则图中全等的三角形有( )
如图,AB=CD,AD=BC,E,F是AC上两点,且AE=CF,则图中全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
分析 由AB=CD,BC=DA且AC为公共边,根据SSS易证得△ACD≌△CAB,进而可得∠DAE=∠BCF,且AD=BC,AE=CF,据SAS即可证得△ADE≌△CBF;同理可证得△CDE≌△ABF.
解答 解:∵AB=CD,BC=DA且AC为公共边,
∴△ACD≌△CAB(SSS),
∴∠DAE=∠BCF,∠ACD=∠CAB;
∵AD=BC,AE=CF,且∠DAE=∠BCF,
∴△ADE≌△CBF(SAS);
同理可证得△CDE≌△ABF.
故图中的全等三角形有:△ACD≌△CAB,△ADE≌△CBF,△CDE≌△ABF,
故选:C.
点评 本题考查了全等三角形的判定,解题时注意,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
10.下列运算正确的是( )
| A. | a3+a4=a6 | B. | a3•a2=a6 | C. | (-a)5÷(-a)3=a2 | D. | (a2)3=a5 |
8.a4+a4的结果是( )
| A. | a8 | B. | 2a8 | C. | a16 | D. | 2a4 |
15.下列计算正确的是( )
| A. | 3a-a=2 | B. | -42=-16 | C. | 3a+b=3ab | D. | -5-2=-3 |
5. 如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )
如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )
 如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )
如图,AB∥CD,∠A=38°,∠C=80°,则∠M为( )| A. | 52° | B. | 42° | C. | 10° | D. | 40° |
12.下列函数关系式中:①y=2x+1;②y=$\frac{1}{x}$;③y=$\frac{x+1}{2}$-x;④s=60t;⑤y=100-25x,表示一次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列点中在反比例函数y=$\frac{2}{x}$图象上的是( )
| A. | (-2,1) | B. | (1,-2) | C. | (-2,-2) | D. | (1,2) |
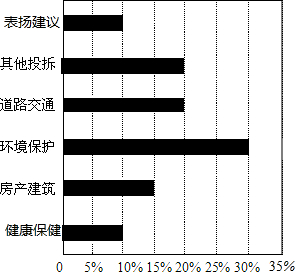 如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.
如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.