题目内容
如图,等腰△OAB的顶角∠AOB=30°,点B在![]() 轴上,腰OA=4.
轴上,腰OA=4.

(1)B点的坐标为: ;
(2)画出△OAB关于![]() 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
(3)求出经过A1点的反比例函数解析式.
(注:若涉及无理数,请用根号表示)
(1)(4,0),(2)(-2,2),(-4,0)(3)
=-
解析:解:(1)(4,0);…………………………………………………………1分
(2)如图1,过点A作AC⊥轴于C点.………………………………2分
在Rt△OAC中,∵斜边OA=4,∠AOB=30°,
∴AC=2,OC=OA·cos30°=2,……………………………4分
∴点A的坐标为(2,2).………………………………………………5分
由轴对称性,得A点关于轴的对称点
A1的坐标为(-2![]() ,2),………………………………………………6分
,2),………………………………………………6分
B点关于轴的对称点B1的坐标为(-4,0);…………………………7分
(3)设过A1点的反比例函数解析式=
,……………………………8分
把点A1的坐标(-2,2)代入解析式,
得2=,∴
=-4
,………………………………………………9分
从而该反比例函数的解析式为 =-
=-![]() .…………………………………10分
.…………………………………10分
(1)通过OA=OB求出B点的坐标
(2)找出对称点,顺次连接,过点A作AC⊥![]() 轴于C点,根据解直角三角形求出OC的长,从而求出A、B两点坐标,再根据对称性求出A1与B1的坐标
轴于C点,根据解直角三角形求出OC的长,从而求出A、B两点坐标,再根据对称性求出A1与B1的坐标
(3)把点A1的坐标代入解析式即可求出

练习册系列答案
相关题目
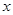 轴上,腰OA=4.
轴上,腰OA=4.
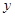 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标; 轴上,腰OA=4.
轴上,腰OA=4.
 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;