题目内容
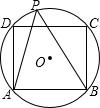如图所示，⊙O是正方形ABCD的外接圆，P是⊙O上不与A、B重合的任意一点，则∠APB等于
- A.45°
- B.60°
- C.45° 或135°
- D.60° 或120°
C
分析：首先连接OA，OB，由⊙O是正方形ABCD的外接圆，即可求得∠AOB的度数，又由圆周角定理，即可求得∠APB的度数．
解答：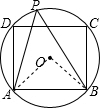
解：连接OA，OB，
∵⊙O是正方形ABCD的外接圆，
∴∠AOB=90°，
若点P在优弧ADB上，则∠APB=
∠AOB=45°；
若点P在劣弧AB上，
则∠APB=180°-45°=135°．
∴∠APB=45°或135°．
故选C．
点评：此题考查了圆周角定理以及正多边形与圆的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与分类讨论思想的应用．
分析：首先连接OA，OB，由⊙O是正方形ABCD的外接圆，即可求得∠AOB的度数，又由圆周角定理，即可求得∠APB的度数．
解答：
解：连接OA，OB，∵⊙O是正方形ABCD的外接圆，
∴∠AOB=90°，
若点P在优弧ADB上，则∠APB=
∠AOB=45°；若点P在劣弧AB上，
则∠APB=180°-45°=135°．
∴∠APB=45°或135°．
故选C．
点评：此题考查了圆周角定理以及正多边形与圆的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与分类讨论思想的应用．
练习册系列答案
相关题目
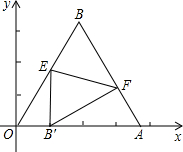正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．
如图所示，△OAB是边长为
的等边三角形，其中O是坐标原点，顶点A在x轴的
正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．
的等边三角形，其中O是坐标原点，顶点A在x轴的正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．
的等边三角形，其中O是坐标原点，顶点A在x轴的正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．