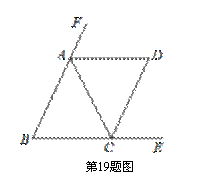题目内容
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.

(1)证明:如图1,连接OD、OE、ED.
∵BC与⊙O相切于一点D,
∴OD⊥BC,
∴∠ODB=90°=∠C,
∴OD∥AC,
∵∠B=30°,
∴∠A=60°,
∵OA=OE,
∴△AOE是等边三角形,
∴AE=AO=0D,
∴四边形AODE是平行四边形,
∵OA=OD,
∴四边形AODE是菱形.
(2)解:设⊙O的半径为r.
∵OD∥AC,
∴△OBD∽△ ABC.
ABC.
∴ ,即8r=6(8﹣r).
,即8r=6(8﹣r).
解得r= ,
,
∴⊙O的半径为 .
.
如图2,连接OD、DF.
∵OD∥AC,
∴∠DAC=∠ADO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAC=∠DAO,
∵AF是⊙O的直径,
∴∠ADF=90°=∠C,
∴△ADC∽△AFD,
∴ ,
,
∴AD2=AC•AF,
∵AC=6,AF= ,
,
∴AD2= ×6=45,
×6=45,
∴AD= =3
=3 .
.



练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 的算术平方根是( )
的算术平方根是( )
|
| A. | 2 | B. | ±2 | C. |
| D. | ± |
某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
|
| A. | 20% | B. | 40% | C. | ﹣220% | D. | 30% |




 .
. |+
|+ +(﹣2)0;
+(﹣2)0;
 是关于
是关于 的一元二次方程,则( )
的一元二次方程,则( ) B.
B.
 且
且 D.
D.