题目内容
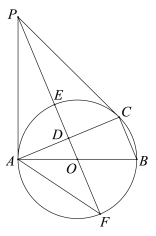
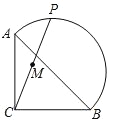
【题目】如图,在等腰 Rt△ABC 中,AC=BC= 2![]() ,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
A. 2 B. 2 ![]() C. π D.
C. π D. ![]() π
π
【答案】C
【解析】
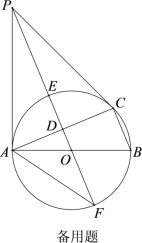
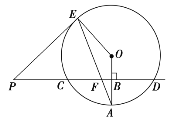
取AC的中点D,BC的中点E,连接DE,则点M的运动轨迹是以DE为直径的半圆.证明![]() 是等腰直角三角形,再利用勾股定理得出半圆半径,最后利用弧长公式即可求解.
是等腰直角三角形,再利用勾股定理得出半圆半径,最后利用弧长公式即可求解.
如图所示,取AC的中点D,BC的中点E,连接DE,则点M的运动轨迹是以DE为直径的半圆.在等腰![]() 中,AC=BC,
中,AC=BC,![]() ,因为D,E分别是AC,BC的中点,所以CD=CE,且
,因为D,E分别是AC,BC的中点,所以CD=CE,且![]() ,故
,故![]() 是等腰直角三角形.在
是等腰直角三角形.在![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,故小半圆的半径r=1.根据圆的弧长公式
,故小半圆的半径r=1.根据圆的弧长公式![]() 得,点M运动的路径长为
得,点M运动的路径长为![]() .
.

故本题正确答案为C.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
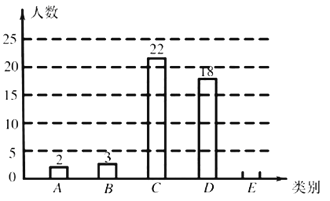
【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.