题目内容
 如图,点E为边长为4的正方形ABCD的边BC的中点,连接AE,过点E作EF⊥AE交CD于点F,则EF的长度为
如图,点E为边长为4的正方形ABCD的边BC的中点,连接AE,过点E作EF⊥AE交CD于点F,则EF的长度为| 5 |
| 5 |
分析:有正方形的性质和垂直的定义可证明△ABE∽△ECF,根据勾股定理求出AE的长,再利用相似三角形的性质:对应边的比值相等即可求出EF的长.
解答:解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠AEB+∠BAE=90°
∵EF⊥AE,
∴∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF,
∴
=
,
在Rt△ABE中,AB=4,BE=
BC=2,
∴AE=
=2
,
∴
=
,
∴EF=
,
故答案为:
∴∠B=∠C=90°,
∵∠AEB+∠BAE=90°
∵EF⊥AE,
∴∠AEF=90°,

∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF,
∴
| AB |
| CE |
| AE |
| EF |
在Rt△ABE中,AB=4,BE=
| 1 |
| 2 |
∴AE=
| 20 |
| 5 |
∴
| 4 |
| 2 |
2
| ||
| EF |
∴EF=
| 5 |
故答案为:
| 5 |
点评:本题主要考查了相似三角形的判定及性质,其中又涉及正方形的一些性质问题,能够熟练掌握.

练习册系列答案
相关题目
 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒( ).
).

 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由. 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒( ).
).
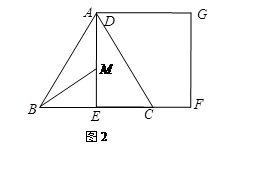
 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由. 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由
