题目内容
如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
(1)求抛物线的解析式;
(2)求cos∠CAB的值和⊙O1的半径;
(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC![]() ,请直接写出所有符合条件的点N的坐标.
,请直接写出所有符合条件的点N的坐标.

【考点】二次函数综合题.
【专题】
【分析】(1)利用待定系数法求出抛物线的解析式;
(2)如答图1所示,由△AOC为等腰直角三角形,确定∠CAB=45°,从而求出其三角函数值;由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度;
 (3)如答图2所示,首先利用圆及抛物线的对称性求出点D坐标,进而求出点M的坐标和线段BM的长度;点B、P、C的坐标已知,求出线段BP、BC、PC的长度;然后利用△BMN∽△BPC相似三角形比例线段关系,求出线段BN和MN的长度;最后利用两点间的距离公式,列出方程组,求出点N的坐标.
(3)如答图2所示,首先利用圆及抛物线的对称性求出点D坐标,进而求出点M的坐标和线段BM的长度;点B、P、C的坐标已知,求出线段BP、BC、PC的长度;然后利用△BMN∽△BPC相似三角形比例线段关系,求出线段BN和MN的长度;最后利用两点间的距离公式,列出方程组,求出点N的坐标.
【解答】解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
∴![]() ,
,
解得a=1,b=4,
∴抛物线的解析式为:y=x2+4x+3.
(2)由(1)知,抛物线解析式为:y=x2+4x+3,
∵令x=0,得y=3,
∴C(0,3),
∴OC=OA=3,则△AOC为等腰直角三角形,
∴∠CAB=45°,
∴cos∠CAB=![]() .
.
在Rt△BOC中,由勾股定理得:BC=![]() .
.
如答图1所示,连接O1B、O1B,
由圆周角定理得:∠BO1C=2∠BAC=90°,
∴△BO1C为等腰直角三角形,
∴⊙O1的半径O1B=![]() BC=
BC=![]() .
.
(3)抛物线y=x2+4x+3=(x+2)2-1,
∴顶点P坐标为(-2,-1),对称轴为x= -2.
 又∵A(-3,0),B(-1,0),可知点A、B关于对称轴x=2对称.
又∵A(-3,0),B(-1,0),可知点A、B关于对称轴x=2对称.
如答图2所示,由圆及抛物线的对称性可知:点D、点C(0,3)关于对称轴对称,
∴D(-4,3).
又∵点M为BD中点,B(-1,0),
∴M(![]() ,
,![]() ),
),
∴BM=![]() ;
;
在△BPC中,B(-1,0),P(-2,-1),C(0,3),
由两点间的距离公式得:BP=![]() ,BC=
,BC=![]() ,PC=
,PC=![]() .
.
∵△BMN∽△BPC,
∴![]() ,即
,即 ,
,
解得:![]() ,MN
,MN![]() .
.
设N(x,y),由两点间的距离公式可得:
 ,
,
解之得, ,
,
∴点N的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【点评】本题综合考查了二次函数的图象与性质、待定系数法、圆的性质、相似三角形、勾股定理、两点间的距离公式等重要知识点,涉及的考点较多,试题难度较大.难点在于第(3)问,需要认真分析题意,确定符合条件的点N有两个,并画出草图;然后寻找线段之间的数量关系,最终正确求得点N的坐标.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案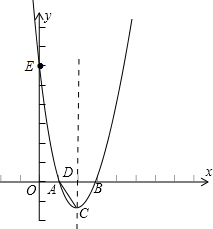 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=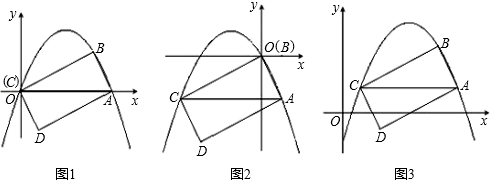
 如图,将抛物线
如图,将抛物线