题目内容
已知在△ABC中,∠C=90°,BC=8,AB=10,点G为重心,那么tan∠GCB的值为________.

分析:作出草图,连接CG并延长交AB于点D,根据重心定义可知点CD是△ABC的中线,求出CD,BD的长度,再过点D作DE⊥BC于点E,根据等腰三角形三线合一的性质求出CE的长度,再利用勾股定理求出DE的长度,然后根据锐角三角函数的定义进行解答即可.
解答:
 解:如图,连接CG并延长交AB于点D,
解:如图,连接CG并延长交AB于点D,∵点G为重心,
∴CD是△ABC的中线,
∴CD=BD=
 AB=
AB= ×10=5,
×10=5,过点D作DE⊥BC于点E,
则CE=BE=
 BC=
BC= ×8=4,
×8=4,在Rt△CDE中,DE=
 =
= =3,
=3,∴tan∠GCB=
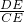 =
= .
.故答案为:
 .
.点评:本题考查了三角形的重心,锐角三角函数的定义,明确三角形的重心是三边中线的交点,并作出辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.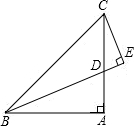 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.