题目内容
已知二次函数y=| 1 | 2 |
(1)求这个二次函数解析式;
(2)设D为线段OC上的点,满足∠DPC=∠BAC,求点D的坐标.
分析:(1)将A、B的坐标代入抛物线中,即可求出二次函数的解析式.
(2)先求得P、C两点坐标,然后通过证△BAC和△PCD来求出CD的长,即可得出D点的坐标.
(2)先求得P、C两点坐标,然后通过证△BAC和△PCD来求出CD的长,即可得出D点的坐标.
解答:解:(1)已知抛物线过A(-3,6),B(-1,0)则有:
解得
∴二次函数的解析式为:y=
x2-x-
;
(2)易知:P(1,-2),C(3,0),
过P作PM⊥x轴于M,
则PM=2,
∵抛物线过C(3,0)和B(-1,0),
∴BC=4,CM=2=PM,
∴∠PCO=45°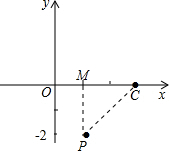
同理可求得∠ACB=45°,
∵∠DPC=∠BAC,∠PCO=∠ACB=45°,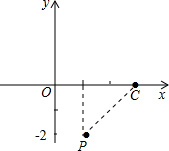
∴△DPC∽△BAC,
∴
=
易求AC=6
,PC=2
,BC=4
∴CD=
,OD=3-
=
∴D(
,0).
|
解得
|
∴二次函数的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)易知:P(1,-2),C(3,0),
过P作PM⊥x轴于M,
则PM=2,
∵抛物线过C(3,0)和B(-1,0),
∴BC=4,CM=2=PM,
∴∠PCO=45°

同理可求得∠ACB=45°,
∵∠DPC=∠BAC,∠PCO=∠ACB=45°,

∴△DPC∽△BAC,
∴
| DC |
| BC |
| PC |
| AC |
易求AC=6
| 2 |
| 2 |
∴CD=
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
∴D(
| 5 |
| 3 |
点评:本题考查了二次函数解析式的确定、相似三角形的判定和性质等知识点.

练习册系列答案
相关题目
已知二次函数y=x2+px+q(p,q为常数,△=p2-4q>0)的图象与x轴相交于A(x1,0),B(x2,0)两点,且A,B两点间的距离为d,例如,通过研究其中一个函数y=x2-5x+6及图象(如图),可得出表中第2行的相关数据.
(1)在表内的空格中填上正确的数;
(2)根据上述表内d与△的值,猜想它们之间有什么关系?再举一个符合条件的二次函数,验证你的猜想;
(3)对于函数y=x2+px+q(p,q为常数,△=p2-4q>0)证明你的猜想.聪明的小伙伴:你能再给出一 种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
(1)在表内的空格中填上正确的数;
(2)根据上述表内d与△的值,猜想它们之间有什么关系?再举一个符合条件的二次函数,验证你的猜想;
(3)对于函数y=x2+px+q(p,q为常数,△=p2-4q>0)证明你的猜想.聪明的小伙伴:你能再给出一
 种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
| y=x2+px+q | p | q | △ | x1 | x2 | d | ||||||||
| y=x2-5x+6 | -5 | 6 | 1 | 2 | 3 | 1 | ||||||||
y=x2-
|
-
|
|
|
|||||||||||
| y=x2+x-2 | -2 | -2 | 3 |
 锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.
锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=-
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=-