题目内容
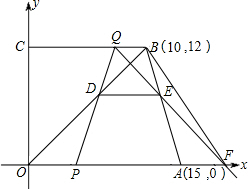
如图,在直角梯形OABC中,AB∥OC,过点O、点B的直线解析式为y= x,OA、AB是方程x2-14x+48=0的两个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
x,OA、AB是方程x2-14x+48=0的两个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.(1)求BC和OC的长;
(2)求y与x的函数关系式;
(3)是否存在x的值,使以点B、点D、点E为顶点的三角形为等腰三角形?若存在,请直接写出x的值;若不存在,请说明理由.

【答案】分析:(1)过点B作BM⊥OC于点M.先解方程x2-14x+48=0,得x1=6,x2=8,再根据直线OB的解析式为y= x,求出BM=8,OM=6,则由勾股定理得到BC=OB=10,由等腰三角形三线合一的性质得到OC=2OM=12;
x,求出BM=8,OM=6,则由勾股定理得到BC=OB=10,由等腰三角形三线合一的性质得到OC=2OM=12;
(2)先由平行线的性质及已知条件证出∠BOC=∠BCO,再结合三角形外角的性质得到∠ODE=∠CBD,则△ODE∽△CBD,根据相似三角形对应边成比例即可求出y与x的函数关系式;
(3)由于∠BED>∠BOC=∠BDE,所以BD>BE,当△BDE为等腰三角形时,分两种情况讨论:①DE=DB,②EB=ED.这两种情况,都可以根据△ODE∽△CBD,对应线段成比例列出方程,求解即可.
解答: 解:(1)解方程x2-14x+48=0,
解:(1)解方程x2-14x+48=0,
得x1=6,x2=8.
过点B作BM⊥OC于点M,
又∵过点O、点B的直线解析式为 ,
,
∴BM:OM=4:3,
∴BM=8,OM=6,
∴BC=OB= ,OC=2OM=12;
,OC=2OM=12;
(2)∵AB∥OC,∴∠ABO=∠BOC,
∵BO=BC,∴∠BOC=∠BCO,
∵∠BDE=∠ABO,∴∠BDE=∠BCO,
∵∠ODB=∠ODE+∠BDE=∠CBD+∠BCO,∴∠ODE=∠CBD,
∴△ODE∽△CBD,∴OD:CB=OE:CD,
∴(12-x):10=(10-y):x,
解得y= x2-
x2- x+10(0<x<12);
x+10(0<x<12);
(3)存在x1=2,x2= ,使以点B、点D、点E为顶点的三角形为等腰三角形.理由如下:
,使以点B、点D、点E为顶点的三角形为等腰三角形.理由如下:
∵∠BED>∠BOC=∠BDE,∴BD>BE,
当△BDE为等腰三角形时,分两种情况:
①当DE=DB时,
∵△ODE∽△CBD,
∴OD:CB=DE:BD=1,
∴(12-x):10=1,
解得x=1;
②当EB=ED时,
∵△ODE∽△CBD,
∴OD:CB=OE:CD=DE:BD,
∴(12-x):10=(10-y):x=y:(12-x),
解得x= .
.
故存在x1=2,x2= ,使以点B、点D、点E为顶点的三角形为等腰三角形.
,使以点B、点D、点E为顶点的三角形为等腰三角形.
点评:本题主要考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理,一次函数的性质,综合性较强,难度中等.其中第(2)问证出△ODE∽△CBD是关键,第(3)问运用分类讨论思想是关键.
 x,求出BM=8,OM=6,则由勾股定理得到BC=OB=10,由等腰三角形三线合一的性质得到OC=2OM=12;
x,求出BM=8,OM=6,则由勾股定理得到BC=OB=10,由等腰三角形三线合一的性质得到OC=2OM=12;(2)先由平行线的性质及已知条件证出∠BOC=∠BCO,再结合三角形外角的性质得到∠ODE=∠CBD,则△ODE∽△CBD,根据相似三角形对应边成比例即可求出y与x的函数关系式;
(3)由于∠BED>∠BOC=∠BDE,所以BD>BE,当△BDE为等腰三角形时,分两种情况讨论:①DE=DB,②EB=ED.这两种情况,都可以根据△ODE∽△CBD,对应线段成比例列出方程,求解即可.
解答:
 解:(1)解方程x2-14x+48=0,
解:(1)解方程x2-14x+48=0,得x1=6,x2=8.
过点B作BM⊥OC于点M,
又∵过点O、点B的直线解析式为
 ,
,∴BM:OM=4:3,
∴BM=8,OM=6,
∴BC=OB=
 ,OC=2OM=12;
,OC=2OM=12;(2)∵AB∥OC,∴∠ABO=∠BOC,
∵BO=BC,∴∠BOC=∠BCO,
∵∠BDE=∠ABO,∴∠BDE=∠BCO,
∵∠ODB=∠ODE+∠BDE=∠CBD+∠BCO,∴∠ODE=∠CBD,
∴△ODE∽△CBD,∴OD:CB=OE:CD,
∴(12-x):10=(10-y):x,
解得y=
 x2-
x2- x+10(0<x<12);
x+10(0<x<12);(3)存在x1=2,x2=
 ,使以点B、点D、点E为顶点的三角形为等腰三角形.理由如下:
,使以点B、点D、点E为顶点的三角形为等腰三角形.理由如下:∵∠BED>∠BOC=∠BDE,∴BD>BE,
当△BDE为等腰三角形时,分两种情况:
①当DE=DB时,
∵△ODE∽△CBD,
∴OD:CB=DE:BD=1,
∴(12-x):10=1,
解得x=1;
②当EB=ED时,
∵△ODE∽△CBD,
∴OD:CB=OE:CD=DE:BD,
∴(12-x):10=(10-y):x=y:(12-x),
解得x=
 .
.故存在x1=2,x2=
 ,使以点B、点D、点E为顶点的三角形为等腰三角形.
,使以点B、点D、点E为顶点的三角形为等腰三角形.点评:本题主要考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理,一次函数的性质,综合性较强,难度中等.其中第(2)问证出△ODE∽△CBD是关键,第(3)问运用分类讨论思想是关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 动时间为t(单位:秒).
动时间为t(单位:秒).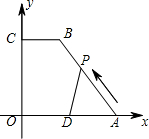 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
 单位,移动时间记为t秒.
单位,移动时间记为t秒. 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.