题目内容
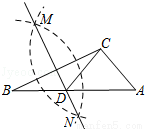
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°?∠ABC,∠DBC=90°?∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23
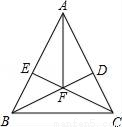
如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
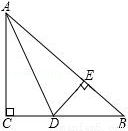
(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
练习册系列答案
相关题目


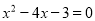 的两根为m,n,则
的两根为m,n,则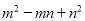 = .
= .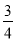 x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )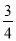 ) D. ( 0,
) D. ( 0, 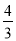 )
)
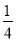 )2 016×161 008;
)2 016×161 008;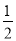 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;