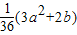题目内容
已抛物线y=3x2+ax+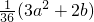
(1)甲学生说:当a取任何不同的数值时,所对应的抛物线都有完全相同的形状;乙学生说:a取不同的数值时,所对应的抛物线的形状也不同.你认为哪位学生说法正确,为什么?
(2)若取a=-2,a=3时所对应的抛物线的顶点分别为A、B.请你求出直线AB的解析式.并判断:当a取其它实数时,所对应的抛物线的顶点是否也在直线AB上?说明理由.
解:(1)根据y=3x2+ax+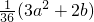 ,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同.
,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同.
(2)当a=-2时,抛物线为y=3x2-2x+ (12+2b),顶点坐标为(
(12+2b),顶点坐标为( ,
, b);
b);
当a=3时,抛物线为y=3x2+3x+ (27+2b),顶点坐标为(-
(27+2b),顶点坐标为(- ,
, b);
b);
设直线AB的解析式为y=kx+n,则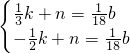 ,
,
解得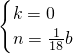 .
.
即直线AB的解析式为y= b.
b.
当a取其它实数时,所对应的抛物线的顶点也在直线AB上.理由如下:
∵抛物线y=3x2+ax+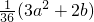 的顶点坐标为(-
的顶点坐标为(- ,
, b),
b),
∴无论a取何值,此抛物线的顶点纵坐标都是 b,
b,
即顶点在直线y= b上.
b上.
故当a取其它实数时,所对应的抛物线的顶点也在直线AB上.
分析:(1)根据y=3x2+ax+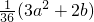 ,二次项系数3决定抛物线的开口方向和大小,即可判断对错.
,二次项系数3决定抛物线的开口方向和大小,即可判断对错.
(2)先求出点A及B的坐标,根据待定系数法求出直线AB的解析式再进行下一步的判断.
点评:本题考查了二次函数图象与系数的关系,待定系数法求函数的解析式及判定一个点在直线上的方法.由于本题运用待定系数法求出的函数y= b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度.
b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度.
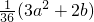 ,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同.
,二次项系数3决定抛物线的开口方向和大小,所以a取任何不同的数值时,对应的抛物线的形状完全相同.(2)当a=-2时,抛物线为y=3x2-2x+
 (12+2b),顶点坐标为(
(12+2b),顶点坐标为( ,
, b);
b);当a=3时,抛物线为y=3x2+3x+
 (27+2b),顶点坐标为(-
(27+2b),顶点坐标为(- ,
, b);
b);设直线AB的解析式为y=kx+n,则
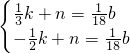 ,
,解得
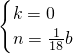 .
.即直线AB的解析式为y=
 b.
b.当a取其它实数时,所对应的抛物线的顶点也在直线AB上.理由如下:
∵抛物线y=3x2+ax+
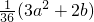 的顶点坐标为(-
的顶点坐标为(- ,
, b),
b),∴无论a取何值,此抛物线的顶点纵坐标都是
 b,
b,即顶点在直线y=
 b上.
b上.故当a取其它实数时,所对应的抛物线的顶点也在直线AB上.
分析:(1)根据y=3x2+ax+
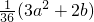 ,二次项系数3决定抛物线的开口方向和大小,即可判断对错.
,二次项系数3决定抛物线的开口方向和大小,即可判断对错.(2)先求出点A及B的坐标,根据待定系数法求出直线AB的解析式再进行下一步的判断.
点评:本题考查了二次函数图象与系数的关系,待定系数法求函数的解析式及判定一个点在直线上的方法.由于本题运用待定系数法求出的函数y=
 b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度.
b是常数函数,此知识点初中教材不要求掌握,因此本题属于竞赛题型,有一定难度. 
练习册系列答案
相关题目
 m(m>O)与x轴交于点D.
m(m>O)与x轴交于点D.