ΧβΡΩΡΎ»ί
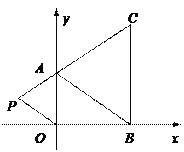
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏlΘΚy=x©¹ ![]() ”κx÷α’ΐΑκ÷αΓΔy÷αΗΚΑκ÷αΖ÷±πœύΫΜ”ΎAΓΔCΝΫΒψΘ§≈ΉΈοœΏy=
”κx÷α’ΐΑκ÷αΓΔy÷αΗΚΑκ÷αΖ÷±πœύΫΜ”ΎAΓΔCΝΫΒψΘ§≈ΉΈοœΏy= ![]() x2+bx+cΨ≠ΙΐΒψBΘ®©¹1Θ§0Θ©ΚΆΒψCΘ°
x2+bx+cΨ≠ΙΐΒψBΘ®©¹1Θ§0Θ©ΚΆΒψCΘ°
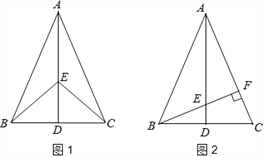
Θ®1Θ©ΧνΩ’ΘΚ÷±Ϋ”–¥≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΚΘΜ
Θ®2Θ©“―÷ΣΒψQ «≈ΉΈοœΏy= ![]() x2+bx+c‘ΎΒΎΥΡœσœόΡΎΒΡ“ΜΗωΕ·ΒψΘ°
x2+bx+c‘ΎΒΎΥΡœσœόΡΎΒΡ“ΜΗωΕ·ΒψΘ°
ΔΌ»γΆΦΘ§Ν§Ϋ”AQΓΔCQΘ§…ηΒψQΒΡΚαΉχ±ξΈΣtΘ§ΓςAQCΒΡΟφΜΐΈΣSΘ§«σS”κtΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωSΒΡΉν¥σ÷ΒΘΜ
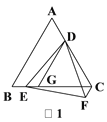
ΔΎΝ§Ϋ”BQΫΜAC”ΎΒψDΘ§Ν§Ϋ”BCΘ§“‘BDΈΣ÷±ΨΕΉςΓ―IΘ§Ζ÷±πΫΜBCΓΔAB”ΎΒψEΓΔFΘ§Ν§Ϋ”EFΘ§«σœΏΕΈEFΒΡΉν–Γ÷ΒΘ§≤Δ÷±Ϋ”–¥≥ω¥Υ ±QΒψΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©y= ![]() x2©¹
x2©¹ ![]() x©¹
x©¹ ![]()
Θ®2Θ©
ΫβΘΚΔΌΉςQMΓΈy÷αΫΜ÷±œΏAC”ΎMΘ§»γΆΦΔΌΘ§
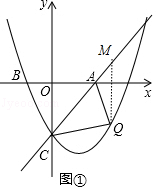
…ηQΘ®tΘ§ ![]() t2©¹
t2©¹ ![]() t©¹
t©¹ ![]() Θ©Θ§‘ρMΘ®tΘ§t©¹
Θ©Θ§‘ρMΘ®tΘ§t©¹ ![]() Θ©Θ§
Θ©Θ§
ΓύMQ=t©¹ ![]() ©¹Θ®
©¹Θ® ![]() t2©¹
t2©¹ ![]() t©¹
t©¹ ![]() Θ©=©¹
Θ©=©¹ ![]() t2+
t2+ ![]() tȧ
tȧ
ΓύS=SΓςCMQ©¹SΓςAMQ= ![]() MQ1=©¹
MQ1=©¹ ![]() t2+
t2+ ![]() t=©¹
t=©¹ ![]() Θ®t©¹1Θ©2+
Θ®t©¹1Θ©2+ ![]() Θ§
Θ§
Β±t=1 ±Θ§S”–Ήν¥σ÷Β ![]() ΘΜ
ΘΜ
ΔΎΝ§Ϋ”OEΓΔOFΘ§ΉςOHΓΆEF”ΎHΘ§»γΆΦΔΎΘ§‘ρEH=FHΘ§

‘ΎRtΓςOBC÷–Θ§ΓΏtanΓœOBC= ![]() =
= ![]() Θ§
Θ§
ΓύΓœOBC=60ΓψΘ§
Ά§άμΩ…ΒΟΓœOAC=60ΓψΘ§AC=2OA=2Θ§
ΓύΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓΏΓœEIF=2ΓœEBFΘ§
ΓύΓœEIF=120ΓψΘ§
ΓύΓœIEH=30ΓψΘ§
‘ΎRtΓςIEH÷–Θ§ΓΏcosΓœIEH= ![]() Θ§
Θ§
ΓύEH= ![]() IEΘ§
IEȧ
ΓύEF=2EH= ![]() IEΘ§
IEȧ
ΕχIE= ![]() BD
BD
ΓύEF= ![]() BDΘ§
BDȧ
Β±BDΒΡ÷ΒΉν–Γ ±Θ§EFΒΡ÷ΒΉν–ΓΘ§
ΕχΒ±BDΓΆAC ±Θ§Φ¥BDΈΣΒ»±ΏΓςABCΒΡΗΏ ±Θ§BDΒΡ÷ΒΉν–ΓΘ§
¥Υ ±BD= ![]() AC=
AC= ![]() Θ§
Θ§
ΓύœΏΕΈEFΒΡΉν–Γ÷ΒΈΣ ![]() Θ§
Θ§
ΓΏΓœQBA=30ΓψΘ§
Γύ÷±œΏBQ”κy÷αΒΡΫΜΒψΈΣΘ®0Θ§©¹ ![]() Θ©Θ§
Θ©Θ§
“ΉΒΟ÷±œΏBQΒΡΫβΈω ΫΈΣy=©¹ ![]() x©¹
x©¹ ![]() Θ§
Θ§
ΫβΖΫ≥ΧΉι 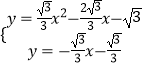 ΒΟ
ΒΟ ![]() Μρ
Μρ ![]() Θ§
Θ§
Γύ¥Υ ±QΒψΒΡΉχ±ξΈΣΘ®2Θ§©¹ ![]() Θ©
Θ©
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©Β±y=0 ±Θ§x©¹ ![]() =0Θ§ΫβΒΟx=
=0Θ§ΫβΒΟx= ![]() Θ§‘ρAΘ®
Θ§‘ρAΘ® ![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
Β±x=0 ±Θ§y=x©¹ ![]() =©¹
=©¹ ![]() Θ§‘ρCΘ®0Θ§©¹
Θ§‘ρCΘ®0Θ§©¹ ![]() Θ©Θ§Α―BΘ®©¹1Θ§0Θ©Θ§CΘ®0Θ§©¹
Θ©Θ§Α―BΘ®©¹1Θ§0Θ©Θ§CΘ®0Θ§©¹ ![]() Θ©¥ζ»κy=
Θ©¥ζ»κy= ![]() x2+bx+cΒΟ
x2+bx+cΒΟ 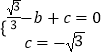 Θ§ΫβΒΟ
Θ§ΫβΒΟ 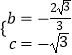 Θ§
Θ§
Υυ“‘≈ΉΈοœΏΫβΈω ΫΈΣy= ![]() x2©¹
x2©¹ ![]() x©¹
x©¹ ![]() ΘΜ
ΘΜ
Υυ“‘¥πΑΗ «y= ![]() x2©¹
x2©¹ ![]() x©¹
x©¹ ![]() ΘΜ
ΘΜ
ΓΨΩΦΒψΨΪΈωΓΩ»œ’φ…σΧβΘ§ Ήœ»–η“ΣΝΥΫβ“Μ¥ΈΚ· ΐΒΡΆΦœσΚΆ–‘÷ (“Μ¥ΈΚ· ΐ «÷±œΏΘ§ΆΦœώΨ≠ΙΐΊμœσœόΘΜ’ΐ±»άΐΚ· ΐΗϋΦρΒΞ,Ψ≠Ιΐ‘≠Βψ“Μ÷±œΏΘΜΝΫΗωœΒ ΐk”κb,Ής”Ο÷°¥σΡΣ–ΓΩ¥Θ§k «–±¬ Ε®Φ–Ϋ«,b”κY÷αά¥œύΦϊ,kΈΣ’ΐά¥”“…œ–±,x‘ωΦθy‘ωΦθΘΜkΈΣΗΚά¥Ήσœ¬’Ι,±δΜ·Ιφ¬…’ΐœύΖ¥ΘΜkΒΡΨχΕ‘÷Β‘Ϋ¥σ,œΏάκΚα÷αΨΆ‘Ϋ‘Ε)Θ§ΜΙ“Σ’ΤΈ’Εΰ¥ΈΚ· ΐΒΡΆΦœσ(Εΰ¥ΈΚ· ΐΆΦœώΙΊΦϋΒψΘΚ1ΓΔΩΣΩΎΖΫœρ2ΓΔΕ‘≥Τ÷α 3ΓΔΕΞΒψ 4ΓΔ”κx÷αΫΜΒψ 5ΓΔ”κy÷αΫΜΒψ)ΒΡœύΙΊ÷Σ Ε≤≈ «¥πΧβΒΡΙΊΦϋΘ°

 νΦΌΉς“Β νΦΌΩλά÷ΝΖΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“Β νΦΌΩλά÷ΝΖΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ –¬ΜνΝΠΉήΕ·‘± νœΒΝ–¥πΑΗ
–¬ΜνΝΠΉήΕ·‘± νœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥–ΘΈΣΗϋΚΟΒΊ≈ύ―χ―ß…ζ–Υ»ΛΘ§ΩΣ’ΙΓΑΆΊ’ΙΩΈ≥ΧΉΏΑύ―ΓΩΈΓ±ΜνΕ·Θ§ΥφΜζ≥ι≤ιΝΥ≤ΩΖ÷―ß…ζΘ§ΝΥΫβΥϊΟ«Ήνœ≤Α°ΒΡœνΡΩάύ–ΆΘ®Ζ÷ΈΣ ιΖ®ΓΔΈßΤεΓΔœΖΨγΓΔΙζΜ≠Ι≤4άύΘ©Θ§≤ΔΫΪΆ≥ΦΤΫαΙϊΜφ÷Τ≥…»γΆΦ≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ±μΦΑΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ° Ήνœ≤Α°ΒΡ¥ΪΆ≥ΈΡΜ·œνΡΩάύ–ΆΤΒ ΐΖ÷≤Φ±μ
œνΡΩάύ–Ά | ΤΒ ΐ | ΤΒ¬ |
ιΖ®άύ | 18 | a |
ΈßΤεάύ | 14 | 0.28 |
œ≤Ψγάύ | 8 | 0.16 |
ΙζΜ≠άύ | b | 0.20 |
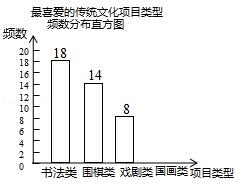
ΗυΨί“‘…œ–≈œΔΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΤΒ ΐΖ÷≤Φ±μ÷–a= Θ§ b=ΘΜ
Θ®2Θ©≤Ι»ΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®3Θ©»τ»Ϊ–ΘΙ≤”–―ß…ζ1500ΟϊΘ§ΙάΦΤΗΟ–ΘΉνœ≤Α°ΈßΤεΒΡ―ß…ζ¥σ‘Φ”–Εύ…Ό»ΥΘΩ