题目内容
探索:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1
(1)观察上面的式子,试求26+25+24+23+22+2+1的值;
(2)试确定22024+22013+22012+…+22+2+1的个位数字.
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1
(1)观察上面的式子,试求26+25+24+23+22+2+1的值;
(2)试确定22024+22013+22012+…+22+2+1的个位数字.
考点:尾数特征
专题:
分析:(1)原式变形后,利用得出的规律计算即可得到结果;
(2)原式变形后,利用得出的规律计算得到结果,再根据2n的个位数字是2,4,8,6,四个一循环,即可求解.
(2)原式变形后,利用得出的规律计算得到结果,再根据2n的个位数字是2,4,8,6,四个一循环,即可求解.
解答:解:(1)原式=(2-1)(26+25+24+23+22+2+1)
=27-1
=127;
(2)原式=(2-1)(22014+22013+22012+22011+…+22+2+1)
=22015-1,
∵2n的个位数字是2,4,8,6,
2015÷4=503…3,
∴22024+22013+22012+…+22+2+1的个位数字为8-1=7.
=27-1
=127;
(2)原式=(2-1)(22014+22013+22012+22011+…+22+2+1)
=22015-1,
∵2n的个位数字是2,4,8,6,
2015÷4=503…3,
∴22024+22013+22012+…+22+2+1的个位数字为8-1=7.
点评:此题考查了尾数特征、整式的混合运算的应用,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
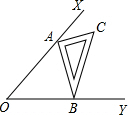 如图,∠XOY=45°,一把直角三角尺△ABC的两个顶点A、B分别在OX,OY上移动,其中AB=10,则点O到顶点A的距离的最大值为
如图,∠XOY=45°,一把直角三角尺△ABC的两个顶点A、B分别在OX,OY上移动,其中AB=10,则点O到顶点A的距离的最大值为 如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.
如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.