题目内容
 图中两个含有30°角的全等直角三角板,分别是Rt△ABC和Rt△BDE,若AC=6,点A、B、D三点在同一直线上,则阴影部分的面积是
图中两个含有30°角的全等直角三角板,分别是Rt△ABC和Rt△BDE,若AC=6,点A、B、D三点在同一直线上,则阴影部分的面积是考点:勾股定理,含30度角的直角三角形
专题:
分析:根据AC=6,结合图形中三角形为含30°的直角三角形,分别求出各边的长度,然后利用三角形的面积公式求得三角形BDE中BD边的高,继而可求得阴影部分的面积.
解答:解:如图所示,在Rt三角形ABC中,
∵AC=6,∠ABC=30°,
∴BC=12,
∴AB=
=6
,
则△BDE中,BD=12,ED=6,BE=6
,
∴EF=
=
=3
,
则S△ABE=
AB•EF=
×6
×3
=27.
故答案为:27.

∵AC=6,∠ABC=30°,
∴BC=12,
∴AB=
| BC2-AC2 |
| 3 |
则△BDE中,BD=12,ED=6,BE=6
| 3 |
∴EF=
| BE•ED |
| BD |
6×6
| ||
| 12 |
| 3 |
则S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:27.
点评:本题考查了勾股定理和含30°角的直角三角形,解答本题的关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半,以及勾股定理的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下列二次根式中,最简二次根式是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在正方形ABCD中,BC=12,∠EBF=45°,若EF=10,则CF的长为( )
如图,在正方形ABCD中,BC=12,∠EBF=45°,若EF=10,则CF的长为( )| A、6 | B、8 | C、4或8 | D、4或6 |
计算(10+
+0.001)2-(0.01+
-10)2的值为( )
| 1 |
| 100 |
| 1 |
| 1000 |
| A、0.44 | B、-1 |
| C、1 | D、-0.44 |
 如图,双曲线y=
如图,双曲线y= 如图,在△AOB中,∠B=25°,将△AOB绕点O顺时针旋转50° 得到△A′OB′,边A′B′与边OB交于点C(点A′不在OB上),则∠A′CO的度数为
如图,在△AOB中,∠B=25°,将△AOB绕点O顺时针旋转50° 得到△A′OB′,边A′B′与边OB交于点C(点A′不在OB上),则∠A′CO的度数为
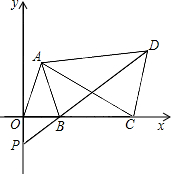 如图,平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且
如图,平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且