题目内容
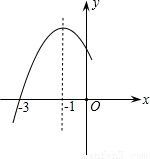
 如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
- A.4+m
- B.m
- C.2m-8
- D.8-2m
C
分析:利用图象可得AB=(点A的横坐标-对称轴)×2解答即可.
解答: 解:因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,
解:因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,
所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A、B两点关于对称轴对称,
因为点A(m,0),且m>4,即AD=m-4,
所以AB=2AD=2(m-4)=2m-8,
故选C.
点评:考查二次函数的两点间距离的求法,注意结合图象.
分析:利用图象可得AB=(点A的横坐标-对称轴)×2解答即可.
解答:
 解:因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,
解:因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A、B两点关于对称轴对称,
因为点A(m,0),且m>4,即AD=m-4,
所以AB=2AD=2(m-4)=2m-8,
故选C.
点评:考查二次函数的两点间距离的求法,注意结合图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
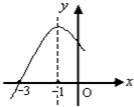 10、已知二次函y=-x2-2x+m的部分图象如图所示,则关于l的一元二次方程-x2-2x+m=0的解为
10、已知二次函y=-x2-2x+m的部分图象如图所示,则关于l的一元二次方程-x2-2x+m=0的解为