��Ŀ����
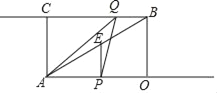
����Ŀ����ͼ����֪����AOBC�У�OB=3����λ��BC=4����λ������P�ӵ�A������������AO��ÿ��4����λ���ȵ��ٶ��˶���ͬʱ����Q�ӵ�B������������BC��ÿ��2����λ���ٶ��˶������˶�ʱ��Ϊt�룮
��1����t��ʾ�߶�PO�ij��ȣ�
��2����tΪ��ֵʱ���ı���APQC�Ǿ��Σ�
��3������APO����AOB���ص����ֵ����Ϊsƽ����λ����s����t�ĺ�����ϵʽ��
��4������P��PE��AO��ֱ��AB�ڵ�E���ڶ���P��Q�˶��Ĺ����У���H��ƽ����һ�㣬����B��Q��E��HΪ������ı���������ʱ����ֱ��д���˶�ʱ��t��ֵ��
���𰸡���1����0��t��1ʱ��PO=4��4t����t��1ʱ��PO=4t��4����2����t= ![]() ʱ���ı���APQC�Ǿ�������3��s��4t;(4)
ʱ���ı���APQC�Ǿ�������3��s��4t;(4) ![]()
��������
(1)��������������п��ǣ�������P���߶�AO�ϣ���P������AO�ϣ�(2)����������ó���AP=4t��CQ=4��2t�����ݾ��ε����ʵó�AP=CQ���Ӷ��ó��𰸣�(3)���١���0��t��1ʱ���ص������ǡ�ADP������DM��OA��M����BC��N���������������Ƶó��𰸣���t��1ʱ���ص��������ı���ADKO����DM��OA��M����BC��N��PQ��OB��K��������������߶εij��ȣ�Ȼ����������(4)����������������м��㣬����BEΪ���εĶԽ��ߣ���BE=BQ����BQ�����εĶԽ��ߣ���BE=BQʱ���ֱ��ĸ�ͼ�Σ��Ӷ��ó��𰸣�
��1����0��t��1ʱ��PO=4��4t����t��1ʱ��PO=4t��4��
��2��AP=4t��CQ=4��2t����APQC�Ǿ���ʱ����AP=CQ�� ��4t=4��2t����t=![]()
��t= ![]() ʱ���ı���APQC�Ǿ��Σ�
ʱ���ı���APQC�Ǿ��Σ�
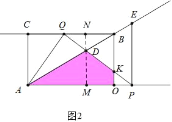
��3������ͼ1�У���0��t��1ʱ���ص������ǡ�ADP����DM��OA��M����BC��N��

��BQ=2t��AP=4t��BQ��AP����![]() =
=![]() =
=![]() =
=![]() �� ��AC=OB=3����DM=
�� ��AC=OB=3����DM=![]() ��3=2��
��3=2��
��s=![]() ��
��
����ͼ2�У���t��1ʱ���ص��������ı���ADKO����DM��OA��M����BC��N��PQ��OB��K��
��OP��BQ����![]() =
=![]() ����
����![]() =
=![]() ����OK=
����OK=![]() ��
��
��![]() ��
��
��4������ͼ3�У���BEΪ���εĶԽ���ʱ��
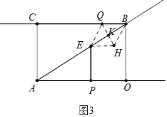
���ı���EQBH�����Σ���EK=BK=![]() ��5��5t������
��5��5t������![]() =cos��ABC=
=cos��ABC=![]() ����
����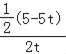 =
=![]() ��
��
��t=![]() ��
��
����ͼ4 �У���BE=BQʱ��
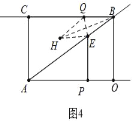
����5��5t=2t��t=![]() ��
��
����ͼ5�У���BQ�����εĶԽ���ʱ��
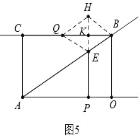
��cos��ABC=![]() ���ɵã�
���ɵã�![]() =
=![]() �����t=
�����t=![]() ��
��
����ͼ6�У���BE=BQʱ��5t��5=2t�����t=![]() ��
��
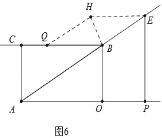
������������������ʱt��ֵΪ![]() ��
��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�