题目内容
 如图,已知△ABC≌△ADE,AD平分∠BAC,且∠BAC=60°,则∠CAE的度数为________.
如图,已知△ABC≌△ADE,AD平分∠BAC,且∠BAC=60°,则∠CAE的度数为________.
30°
分析:根据角平分线的定义求出∠BAD,再根据全等三角形对应角相等可得∠BAC=∠DAE,然后求出∠CAE=∠BAD.
解答:∵AD平分∠BAC,∠BAC=60°,
∴∠BAD= ∠BAC=
∠BAC= ×60°=30°,
×60°=30°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD,
∴∠CAE=30°.
故答案为:30°.
点评:本题考查了全等三角形对应角相等的性质,角平分线的定义,是基础题,熟记性质并准确识图是解题的关键.
分析:根据角平分线的定义求出∠BAD,再根据全等三角形对应角相等可得∠BAC=∠DAE,然后求出∠CAE=∠BAD.
解答:∵AD平分∠BAC,∠BAC=60°,
∴∠BAD=
 ∠BAC=
∠BAC= ×60°=30°,
×60°=30°,∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD,
∴∠CAE=30°.
故答案为:30°.
点评:本题考查了全等三角形对应角相等的性质,角平分线的定义,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
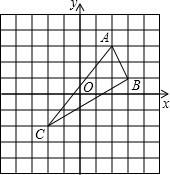
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH. 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°. 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
 20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.
20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.