题目内容
如图,E、F是边长为4的正方形ABCD的边BC、CD上的点,CE=1,CF=| 4 | 3 |
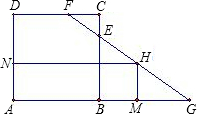 B的延长线于G,过线段FG上的一个动点H,作HM⊥AG,HN⊥AD,垂足为M、N,设HM=x,矩形AMHN的面积为y.
B的延长线于G,过线段FG上的一个动点H,作HM⊥AG,HN⊥AD,垂足为M、N,设HM=x,矩形AMHN的面积为y.(1)求y与x之间的函数关系式;
(2)当x为何值时,矩形AMHN的面积最大,最大面积是多少?
分析:(1)要求矩形的面积,就要得出AM和MH的值,已知了MH为x,关键是求AM的长,那么必须得出BG,MG的长,可根据相似三角形CFE和BGE求出BG的长(也可用BE和∠C的正切值来求).然后在直角三角形GMH中,用HM和∠C的正切值求出MG,这样就能表示出AM的长,就可得出关于x,y的函数关系式.
(2)可根据(1)的函数的性质及自变量的取值范围来求出矩形面积的最大值以及对应的x的值.
(2)可根据(1)的函数的性质及自变量的取值范围来求出矩形面积的最大值以及对应的x的值.
解答:解:(1)∵EC=1,BC=4
∴BE=3
∵CF∥BG,
∴△ECF∽△EBG,
∴
=
即:
=
∴BG=4
在Rt△GMH中,tan∠G=tan∠CFE=
,因此MG=
HM=
x.
∴AM=AG-MG=AB+BG-MG=4+4-
x=8-
x
∴y=x•(8-
x)=-
x2+8x(0<x≤4);
(2)由(1)的函数式可知:y=-
(x-3)2+12
因此当x=3时,矩形AMHN的面积最大,最大值为12.
∴BE=3
∵CF∥BG,
∴△ECF∽△EBG,
∴
| CF |
| BG |
| CE |
| BE |
| ||
| BG |
| 1 |
| 3 |
∴BG=4
在Rt△GMH中,tan∠G=tan∠CFE=
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
∴AM=AG-MG=AB+BG-MG=4+4-
| 4 |
| 3 |
| 4 |
| 3 |
∴y=x•(8-
| 4 |
| 3 |
| 4 |
| 3 |
(2)由(1)的函数式可知:y=-
| 4 |
| 3 |
因此当x=3时,矩形AMHN的面积最大,最大值为12.
点评:本题主要考查了正方形和矩形的性质以及二次函数的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•湛江)如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则an=
(2012•湛江)如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则an=
 (2012•东莞模拟)如图,每个小方格是边长为1各单位长度的小正方形
(2012•东莞模拟)如图,每个小方格是边长为1各单位长度的小正方形 如图,已知P是边长为a的正方形ABCD内一点,△PBC是等边三角形,则△PAD的外接圆半径是( )
如图,已知P是边长为a的正方形ABCD内一点,△PBC是等边三角形,则△PAD的外接圆半径是( )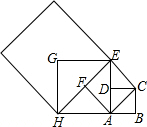 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an的表达式为( )
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an的表达式为( )