题目内容
在Rt△ABC中，已知∠C=90°，∠A=30°，BD是∠B的平分线，AC=18，则BD的值为
- A.
- B.9
- C.12
- D.6
C
分析：求BD的长应利用锐角三角函数算出和直角三角形有关的AD长和CD长即可．
解答：
解：在Rt△ABC中，∠C=90°，∠A=30°，所以∠ABC=60°，
∵BD是∠ABC的平分线，∴∠CBD=30°，
在Rt△ABC中，tan30°=
∴
=
∴BC=
在Rt△CBD中，CD=BC•tan30°=6
∴AD=AC-CD=18-6=12
∵∠A=∠ABD
∴BD=AD=12．
故选C．
点评：解决本题的关键是得到所求的线段的相应线段的长度，主要应用了三角函数值．
分析：求BD的长应利用锐角三角函数算出和直角三角形有关的AD长和CD长即可．
解答：
解：在Rt△ABC中，∠C=90°，∠A=30°，所以∠ABC=60°，∵BD是∠ABC的平分线，∴∠CBD=30°，
在Rt△ABC中，tan30°=
∴
=∴BC=
在Rt△CBD中，CD=BC•tan30°=6
∴AD=AC-CD=18-6=12
∵∠A=∠ABD
∴BD=AD=12．
故选C．
点评：解决本题的关键是得到所求的线段的相应线段的长度，主要应用了三角函数值．
练习册系列答案
相关题目
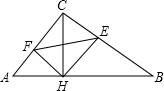如图，在Rt△ABC中，已知∠ACB=90°，且CH⊥AB，HE⊥BC，HF⊥AC．
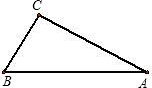如图，在Rt△ABC中，已知∠BCA=90°，∠BAC=30°，AB=6cm．把△ABC以点B为中心逆时针旋转，使点C旋转到AB边的延长线上得到Rt△A1BC1．在Rt△ABC中，已知∠C=90°，∠A=30°，BD是∠B的平分线，AC=18，则BD的值为（ ）
A、3
| ||
| B、9 | ||
| C、12 | ||
| D、6 |
如图，在Rt△ABC中，已知∠ABC=90°，BC=6，以AB为直径作⊙O，连接OC，过点C作⊙O的切线CD，D为切点，若sin∠OCD=
如图，在Rt△ABC中，已知tanB=2，则sinA的值是（ ）