题目内容
(1)A、B、C三个小朋友分别站到如图1所示的三个小三角形中做游戏,若每个小三角形中只站一人.则A、B两人相邻的概率是多少?(2)A、B、C三个小朋友分别站到如图2所示的四个小三角形中做游戏,若每个小三角形中只站一人.则中间的三角形没有站人的概率是多少?

分析:本题是一道列举法求概率的问题,属于基础题,可以直接应用求概率的公式.
解答:解:(1)A、B、C三个小朋友分别站到如图1所示的三个小三角形中做游戏,若每个小三角形中只站一人.
出现的结果有ABC,ACB,BAC,BCA,CAB,CBA,
P(AB相邻)=
=
;
(2)A、B、C三个小朋友分别站到如图2所示的四个小三角形中做游戏,若每个小三角形中只站一人.设中间的三角形为D,
出现的情况如下ABC,ABD,ACD,BAC,BAD,BCD,CAB,CAD,CBD,DAB,DAC,DBC,共12种可能,
P(中间没有站人)=
=
.
出现的结果有ABC,ACB,BAC,BCA,CAB,CBA,
P(AB相邻)=
| 4 |
| 6 |
| 2 |
| 3 |
(2)A、B、C三个小朋友分别站到如图2所示的四个小三角形中做游戏,若每个小三角形中只站一人.设中间的三角形为D,
出现的情况如下ABC,ABD,ACD,BAC,BAD,BCD,CAB,CAD,CBD,DAB,DAC,DBC,共12种可能,
P(中间没有站人)=
| 3 |
| 12 |
| 1 |
| 4 |
点评:本题考查的是概率的求法,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2003个三角形的周长为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
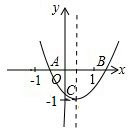 已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
 24、如图给出四个条件:①PA切⊙O于点A;②PB切⊙O于B;③AC为⊙O直径;④弦CB∥PO.
24、如图给出四个条件:①PA切⊙O于点A;②PB切⊙O于B;③AC为⊙O直径;④弦CB∥PO.