题目内容
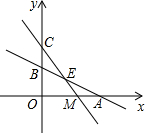 如图:直线AB:y=-
如图:直线AB:y=-| 1 | 2 |
(1)求△COM的面积S与点M的移动时间t的函数关系式;
(2)当t何值时△COM≌△AOB,并求出此时点M的坐标;
(3)记直线AB与CM的交点为点E,问:满足△CBE是等腰三角形的t值共有几个?直接写出满足条件的t值.
分析:(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;分当0≤t≤4时,OM=OA-AM=4-t,当t>4时,OM=AM-OA=t-4,由面积公式求出S与t之间的函数关系式;
(2)若△COM≌△AOB,OM=OB则t时间内移动了AM,可算出t值,并得到M点坐标;
(3)分①BE=BC=2;②CE=BE;③CB=CE;三种情况讨论可求满足△CBE是等腰三角形的t值.
(2)若△COM≌△AOB,OM=OB则t时间内移动了AM,可算出t值,并得到M点坐标;
(3)分①BE=BC=2;②CE=BE;③CB=CE;三种情况讨论可求满足△CBE是等腰三角形的t值.
解答:解:(1)对于直线AB:y=-
x+2,
当x=0时,y=2;
当y=0时,x=4.
则A、B两点的坐标分别为A(4,0)、B(0,2);
∵C(0,4),
∴OC=OA=4,
∴当0≤t≤4时,OM=OA-AM=4-t,S=
×4×(4-t)=8-2t;
当t>4时,OM=AM-OA=t-4,S=
×4×(t-4)=2t-8;
(2)分为两种情况:①当M在OA上时,OB=OM=2,△COM≌△AOB.
∴AM=OA-OM=4-2=2
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间是2秒钟;
M(2,0),
②当M在AO的延长线上时,OM=OB=2,
则M(-2,0),
即M点的坐标是(2,0)或(-2,0).
(3)∵A(4,0)、B(0,2),
∴AB=2
;
①BE=BC=2时,

如图1,BF:2=EF:4=2:2
,
解得BF=
,EF=
,
则
:OM=(2+
):4,
解得OM=2
-2,
则t=4-(2
-2)=6-2
;
如图2,BF:2=EF:4=2:2
,
解得BF=
,EF=
,
则
:OM=(2-
):4,
解得OM=2
+2,
则t=4+(2
+2)=6+2
;
②CE=BE时,
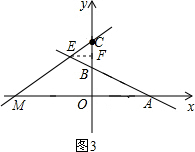
如图3,BF:2=EF:4=1:2,
解得BF=1,EF=2,
则2:OM=1:4,
解得OM=8,
则t=4+8=12;
③CB=CE时,
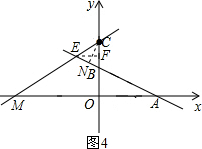
如图4,BN:2=2:2
,解得BN=
,
则BE=
,
BF:2=EF:4=
:2
,
解得BF=
,EF=
,
则
:OM=(2-
):4,
解得OM=
,
则t=4+
=
.
综上所述,满足△CBE是等腰三角形的t值有:6-2
;6+2
;12;
.
| 1 |
| 2 |
当x=0时,y=2;
当y=0时,x=4.
则A、B两点的坐标分别为A(4,0)、B(0,2);
∵C(0,4),
∴OC=OA=4,
∴当0≤t≤4时,OM=OA-AM=4-t,S=
| 1 |
| 2 |
当t>4时,OM=AM-OA=t-4,S=
| 1 |
| 2 |
(2)分为两种情况:①当M在OA上时,OB=OM=2,△COM≌△AOB.
∴AM=OA-OM=4-2=2
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间是2秒钟;
M(2,0),
②当M在AO的延长线上时,OM=OB=2,
则M(-2,0),
即M点的坐标是(2,0)或(-2,0).
(3)∵A(4,0)、B(0,2),
∴AB=2
| 5 |
①BE=BC=2时,

如图1,BF:2=EF:4=2:2
| 5 |
解得BF=
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
则
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
解得OM=2
| 5 |
则t=4-(2
| 5 |
| 5 |
如图2,BF:2=EF:4=2:2
| 5 |
解得BF=
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
则
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
解得OM=2
| 5 |
则t=4+(2
| 5 |
| 5 |
②CE=BE时,

如图3,BF:2=EF:4=1:2,
解得BF=1,EF=2,
则2:OM=1:4,
解得OM=8,
则t=4+8=12;
③CB=CE时,

如图4,BN:2=2:2
| 5 |
| 2 |
| 5 |
| 5 |
则BE=
| 4 |
| 5 |
| 5 |
BF:2=EF:4=
| 4 |
| 5 |
| 5 |
| 5 |
解得BF=
| 4 |
| 5 |
| 8 |
| 5 |
则
| 8 |
| 5 |
| 4 |
| 5 |
解得OM=
| 16 |
| 3 |
则t=4+
| 16 |
| 3 |
| 28 |
| 3 |
综上所述,满足△CBE是等腰三角形的t值有:6-2
| 5 |
| 5 |
| 28 |
| 3 |
点评:此题考查了同学们根据函数图象求坐标,通过动点变化求函数关系式,以及等腰三角形的性质,分类思想的运用.

练习册系列答案
相关题目
 3、如图,直线AB、CD、EF相交于O,图中对顶角共有( )
3、如图,直线AB、CD、EF相交于O,图中对顶角共有( ) 如图,直线AB、CD相交于点O,OE平分∠BOD,∠1=35°,则∠AOC度数是( )
如图,直线AB、CD相交于点O,OE平分∠BOD,∠1=35°,则∠AOC度数是( ) (2013•梧州一模)如图,直线AB和CD相交于点O,若∠AOD=55°,则∠AOC=( )
(2013•梧州一模)如图,直线AB和CD相交于点O,若∠AOD=55°,则∠AOC=( ) 如图,直线AB,CD相交于点O,射线OE平分∠COB,已知∠EOC=60°,求∠AOD与∠BOD的度数.
如图,直线AB,CD相交于点O,射线OE平分∠COB,已知∠EOC=60°,求∠AOD与∠BOD的度数. 如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOE的度数是
如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOE的度数是