题目内容
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(﹣2,3)、B(﹣1,2)、C(﹣3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
(1)在正方形网格中作出△A1B1C1;
(2)在旋转过程中,点A经过的路径 的长度为 ;(结果保留π)
的长度为 ;(结果保留π)
(3)在y轴上找一点D,使DB+DB1的值最小,并求出D点坐标.

(1)在正方形网格中作出△A1B1C1;
(2)在旋转过程中,点A经过的路径
 的长度为 ;(结果保留π)
的长度为 ;(结果保留π)(3)在y轴上找一点D,使DB+DB1的值最小,并求出D点坐标.

解;(1)作图如下:

(2) 。
。
(3)D(0, )。
)。

(2)
 。
。(3)D(0,
 )。
)。试题分析:(1)根据△ABC绕点O顺时针旋转90°后得到△A1B1C1,得出各对应点位置画出图象即可。
(2)利用弧长公式求出点A经过的路径
 的长度即可:
的长度即可:∵在旋转过程中,OA旋转旋转的角度为90°,由勾股定理可得OA=
 ,
,∴点A经过的路径
 的长度为:
的长度为: ,
,(3)利用待定系数法求一次函数解析式进而得出D点坐标。
解;(1)作图如下:

(2)
 。
。(3)∵B,B1在y轴两旁,连接BB1交y轴于点D,
设D′为y轴上异于D的点,显然D′B+D′B1>DB+DB1,∴此时DB+DB1最小。
设直线BB1解析式为y=kx+b,依据题意得出:
 ,解得:
,解得: 。
。∴直线BB1解析式为
 。
。令x=0,得
 。∴D(0,
。∴D(0, )。
)。
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ,为了使白球反弹后能将黑球直接撞入袋中,那么几大白球时,必须保证
,为了使白球反弹后能将黑球直接撞入袋中,那么几大白球时,必须保证 的度数为【 】
的度数为【 】






















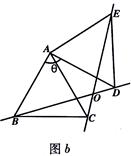

 <180°),得到△ADE,BD和EC所在直线相交于点O.
<180°),得到△ADE,BD和EC所在直线相交于点O. AB′,AC=
AB′,AC=