题目内容
 (2013•巴中)2013年4月20日,四川雅安发生里氏7.0级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距4米,探测线与地面的夹角分别为30°和60°,如图所示,试确定生命所在点C的深度(结果精确到0.1米,参考数据
(2013•巴中)2013年4月20日,四川雅安发生里氏7.0级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距4米,探测线与地面的夹角分别为30°和60°,如图所示,试确定生命所在点C的深度(结果精确到0.1米,参考数据| 2 |
| 3 |
分析:过点C作CD⊥AB交AB于点D,则∠CAD=30°,∠CBD=60°,在Rt△BDC中,CD=
BD,在Rt△ADC中,AD=
CD,然后根据AB=AD-BD=4,即可得到CD的方程,解方程即可.
| 3 |
| 3 |
解答:解:如图,过点C作CD⊥AB交AB于点D.
∵探测线与地面的夹角为30°和60°,
∴∠CAD=30°,∠CBD=60°,
在Rt△BDC中,tan60°=
,
∴BD=
=
,
在Rt△ADC中,tan30°=
,
∴AD=
=
,
∵AB=AD-BD=4,
∴
-
=4,
∴CD=2
≈3.5(米).
答:生命所在点C的深度大约为3.5米.

∵探测线与地面的夹角为30°和60°,
∴∠CAD=30°,∠CBD=60°,
在Rt△BDC中,tan60°=
| CD |
| BD |
∴BD=
| CD |
| tan60° |
| CD | ||
|
在Rt△ADC中,tan30°=
| CD |
| AD |
∴AD=
| CD |
| tan30° |
| 3CD | ||
|
∵AB=AD-BD=4,
∴
| 3CD | ||
|
| CD | ||
|
∴CD=2
| 3 |
答:生命所在点C的深度大约为3.5米.
点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形,解直角三角形,也考查了把实际问题转化为数学问题的能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 (2013•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
(2013•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )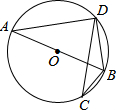 (2013•巴中)如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
(2013•巴中)如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( ) (2013•巴中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
(2013•巴中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) (2013•巴中)△ABC在平面直角坐标系xOy中的位置如图所示.
(2013•巴中)△ABC在平面直角坐标系xOy中的位置如图所示.