题目内容
一条抛物线具有下列特征:(1)经过点A(0,3);(2)在x轴左侧的部分是上升的,在x轴右侧的部分是下降的,试写出一条满足这两条特征的抛物线的表达式: .
y=-x2 +3
试题分析:由题意可知,该条抛物线开口向下,才符合在
 轴左侧的部分是上升的,在y轴右侧的部分是下降的,因为该条抛物线经过点A(0,3),所以符合题意的抛物线有很多,
轴左侧的部分是上升的,在y轴右侧的部分是下降的,因为该条抛物线经过点A(0,3),所以符合题意的抛物线有很多, 就是其中一个
就是其中一个点评:本题属于对抛物线的基本性质和抛物线的定理的知识的熟练把握

练习册系列答案
相关题目

 (a<0)的图象上,则a的值为 ( )
(a<0)的图象上,则a的值为 ( ) 




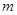 = ,
= ,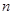 = .
= . 与直线
与直线 相交于O(0,0)和A(3,2)两点,则不等式
相交于O(0,0)和A(3,2)两点,则不等式 的解集为 .
的解集为 .
 的图象如图所示,那么二次函数
的图象如图所示,那么二次函数 的图象大致为( )
的图象大致为( )


 的对称轴是直线
的对称轴是直线 ,且经过点
,且经过点 (3,0),则
(3,0),则 的值为( )
的值为( )