题目内容
 已知:正方形ABCD的对角线AC、BD交于点O,E是OB延长线上一点,∠ECB=15°.
已知:正方形ABCD的对角线AC、BD交于点O,E是OB延长线上一点,∠ECB=15°.
求证:EC=BD.
证明:∵四边形ABCD是正方形,
∴AC⊥BD,BD=2OD=2OC,∠OCB=45°,
∴∠EOC=90°,
∵∠ECB=15°,∠BOC=45°,
∴∠ECO=15°+45°=60°,
∵∠EOC=90°,
∴∠E=90°-60°=30°,
∴EC=2OC,
∵BD=2OC,
∴EC=BD.
分析:根据正方形性质求出AC⊥BD,BD=2OD=2OC,∠OCB=45°,求出∠EOC=90°,∠E=30°,推出EC=2OC,根据BD=2OC即可得出答案.
点评:本题考查了正方形性质,含30度角的直角三角形性质的应用,关键是求出EC=2OC,注意:正方形的对角线相等且互相平分,每一条对角线平分一组对角.
∴AC⊥BD,BD=2OD=2OC,∠OCB=45°,
∴∠EOC=90°,
∵∠ECB=15°,∠BOC=45°,
∴∠ECO=15°+45°=60°,
∵∠EOC=90°,
∴∠E=90°-60°=30°,
∴EC=2OC,
∵BD=2OC,
∴EC=BD.
分析:根据正方形性质求出AC⊥BD,BD=2OD=2OC,∠OCB=45°,求出∠EOC=90°,∠E=30°,推出EC=2OC,根据BD=2OC即可得出答案.
点评:本题考查了正方形性质,含30度角的直角三角形性质的应用,关键是求出EC=2OC,注意:正方形的对角线相等且互相平分,每一条对角线平分一组对角.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )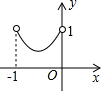
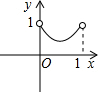
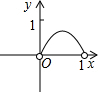
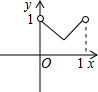
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=